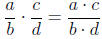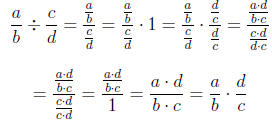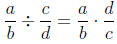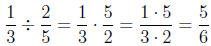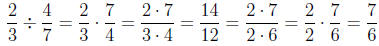|
|
Rational Expressions
Remember rational numbers? The rational numbers are all
real numbers
that can be written as a fraction. Similarly, rational expressions are
expressions that can be written as a fraction. For example,
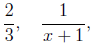 and and
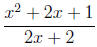
are rational expressions because they are written as a
fraction. Typically, we
talk about rational expressions where the numerator and denominator are
both polynomials.
The Domain of Rational Expressions
Have you ever typed "1 / 0" into your calculator? If you have, it says: "ERROR:
ILLEGAL DIVISION BY ZERO." This is because zero can NOT be
in the denominator of ANY expression. The same thing goes for rational
expressions
that are quotients of polynomials. Therefore, we have a restriction
on the values we can plug in to any rational expression. Specifically, we can
not have a denominator of zero. This means that the expression is undefined
for whatever x values make the denominator equal to zero. In general, the
domain of an algebraic expression is the set of all real numbers for which
the expression is defined. Since rational expressions are undefined when the
denominator is zero, the domain of a rational expression is the set of all real
numbers such that the denominator is not zero.
For example, what is the domain of
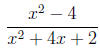
From the definition, it is the set of all real so that x2
+4x+2 ≠ 0. Since this
is hardly ever zero, it will be easier to find when it is equal to zero. Then
the domain is all real numbers except those that make the denominator zero.
Thankfully, we can factor the denominator into
x2 + 5x + 6 = (x + 2)(x + 3) = 0 when x = -3 or x = -2
Therefore, our domain is the set of all real numbers x such that x does
not equal -2 and x does not equal -3. We can write this is set notation as:
{ x ∈ R l x ≠ -3 and x ≠ -2}. This is also sometimes
written as { xl x is a real
number and x ≠ -3 and x ≠ -2}. Sometimes, ":" is used as the separator
instead of "l", it just depends on the book.
Manipulating Rational Expressions
Rational expressions show up in many places in algebra, and it is very important
to be comfortable working with them. This means:
•
simplify rational expressions to make them easier to work with
•
add and subtract rational expressions to look for more simplifications
•
multiply and divide rational expressions to combine them for further
simplification
All of these skills are necessary to effectively work with rational exressions.
These expressions can become cumbersome very quickly, and it is essential
to have these skills mastered in order to use them as tools to solve other
problems rather than the first step you didn't see.
Simplifying Rational Expressions
Simplifying rational expressions is all about multiplying by 1. The trick is
to find all of these factors of 1 hidden in the problem. First, recall that for
any real number x ≠ 0,
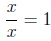
Therefor, whenever we have a factor in the numerator and
denominator that
are the same, we can "cancel" the terms. Consider the example used in the
previous section:
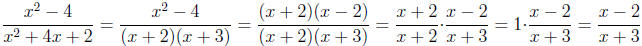
Therefore, we have simplified the domain example:
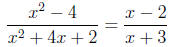
However, the domain of the simplified expression is { x ∈ R
lx ≠ -3}, which
is NOT the same as the original domain. This is because the two expressions
are not quite equal. They are equal when BOTH are defined. In other words,
they are equal for all x that are in BOTH domains. These expressions are
called equivalent expressions because they are not truly equal, but they
have the same value for all numbers that are in both domains. These two
domains are different because the domain of 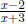 has -2 in its domain, but the has -2 in its domain, but the
original expression 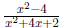 is not defined for this
value because the denominator is not defined for this
value because the denominator
is zero. This leads to an important point. WHEN YOU SIMPLIFY
AN EXPRESSION, YOU DO NOT CHANGE THE DOMAIN!
Arithmetic Operations Involving Rational Expressions
Rational expressions work just like fractions. You add, subtract, multiply
and divide rational expressions the same way you do fractions.
Multiplication is the easiest operation to carry out on fractions. Simply
multipily the numerators to get the new numerator, and multiply the
denominators to get the new denominator. For example:
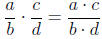
In other words, just multiply straight across to get the
answer.
Division is almost as simple as multiplication. In fact, you can turn a
division problem with fractions into a multiplication problem. For a longwinded
example, consider:
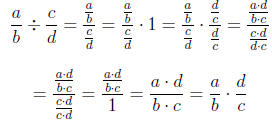
Therefore 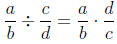
Ok. That was long and laborious. However, we did not break
any of the rules
(provided c ≠ 0 and d ≠ 0, which would make no sense from the beginning
since the initial problem would have division by zero). The bottom line of
that was to show that we can change a division problem into a multiplication
problem if we use the reciprocal of the term we are
dividing by. In other
words, we just " flip the second and multiply." For a concrete example with
numbers:
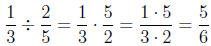
Of course, we would have to reduce this answer if we
could, such as in this
example:
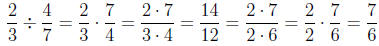
We had to reduce this final answer. It is always good to
reduce the final
answer if it is possible.
|


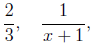 and
and
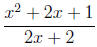
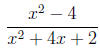
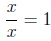
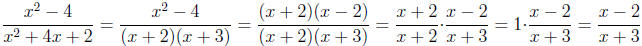
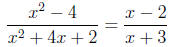
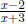 has -2 in its domain, but the
has -2 in its domain, but the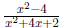 is not defined for this
value because the denominator
is not defined for this
value because the denominator