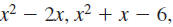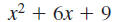|
|
RATIONAL EXPRESSIONS II
Overview
In this lesson, you will learn about negative exponents.
You will also study
scientific notation. Finally, you will learn more about how to multiply,
divide, add, and subtract rational expressions.
Explain
Concept 1 has sections on
• Definition of a Negative
Integer Exponent
• Properties of Negative
Exponents
• Simplifying Expressions
that Contain Negative
Exponents
• Scientific Notation
Recall:
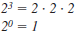
CONCEPT 1:
NEGATIVE EXPONENTS
Definition of a Negative Integer Exponent
You have seen how to work with exponents that are positive integers or 0.
Now, we will investigate exponents that are negative integers.
We’ll begin with this expression: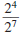
We can simplify the expression by
canceling common factors.
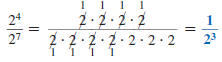
We can also simplify the expression
by subtracting exponents.
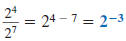
Since 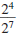 simplifies to
both simplifies to
both 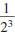 and and 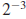 ,
we conclude ,
we conclude 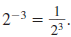
This relationship holds in general.
— Definition —
Negative Integer Exponent
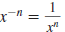
Here, x ≠0 and n is a nonnegative integer. |
Be careful!
Here, 5 is raised to a negative power.
But the result is a positive number.
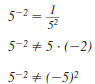
A negative exponent does not determine
if an expression is positive or negative.
For example:
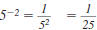 positive positive
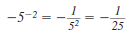 negative negative
Example 8.2.1
Find: 5-2
Solution
Use the definition of a negative exponent:
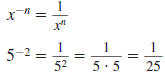
so,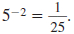
We can also define
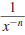 , as follows: , as follows:
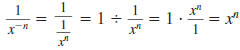
— Definition —
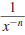
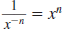
Here, x≠ 0 and n is a nonnegative integer. |
Example 8.2.2
a. Find:
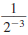
b. Find:
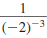
Solution
a. Use the definition
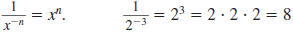
b. Use the definition
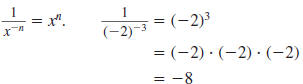
Here is a summary of our work with negative exponents:
Definition
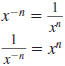
Example 1
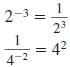
Example 2
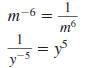
Here, the variables represent nonzero real numbers and n
is a nonnegative
integer.
Example 8.2.3
Find: 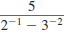
| Solution |
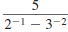 |
Use the definition of a negative exponent,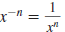 |
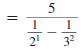 |
| Evaluate the exponential expressions. |
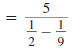 |
In the denominator of the expression, write each
fraction using the LCD, 18. |
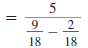 |
In the denominator of the expression, subtract
the fractions. |
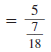 |
| Rewrite the division using ÷. |
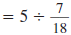 |
To divide 5 by a fraction, multiply 5/1by the
reciprocal of the fraction. |
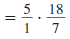 |
| Multiply the numerators and multiply the
denominators. |
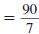 |
Thus,
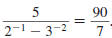
Example 8.2.4
Rewrite using only positive exponents:
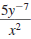
Solution
Since -7 is the exponent of y, not 5y,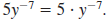 |
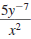 |
Use the definition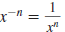 |
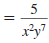 |
Thus,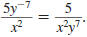
Properties of Negative Exponents
The properties of whole number exponents also hold for negative
exponents. This table contains an example of each property.
| Property |
Positive Integer
Exponents |
Negative Integer
Exponents |
| Multiplication |
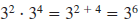 |
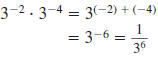 |
| Division |
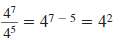 |
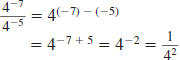 |
Power of a
Power |
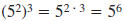 |
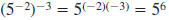 |
Power of a
Product |
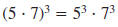 |
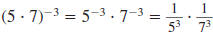 |
Power of a
Quotient |
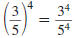 |
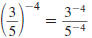 |
Now we will find two additional properties of negative
exponents.
We’ll begin by simplifying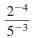 . . |
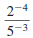 |
| We apply the definition of a negative exponent. |
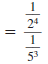 |
| Rewrite the division using÷ |
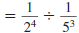 |
| To divide by a fraction, multiply by its
reciprocal. |
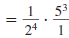 |
| Multiply the numerators. Multiply the
denominators. |
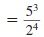 |
Thus,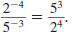
Notice that the bases, 2 and 5, have moved to the opposite
side of the
division bar, and the signs of the their exponents changed.
This turns out to be true in general.
Next, we’ll use this relationship to rewrite a quotient raised to a
negative power.
For example, we’ll simplify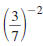 . . |
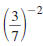 |
| We use the Power of a Quotient Property |
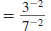 |
As in the previous example, we move each base to
the
opposite side of the division bar and change the sign
of each exponent. |
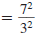 |
| Again, we use the Power of a Quotient Property. |
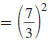 |
We see that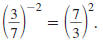
Notice that the new base, 7/3, is the reciprocal of the
original base. Also
notice the new exponent, 2, is the opposite of the original exponent.
— Properties —
To Rewrite a Quotient Using Positive Exponents
A factor that contains a negative exponent may be
rewritten on the
other side of the division bar by changing the sign of the exponent.
Property
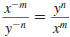
Example 1
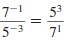
Example 2
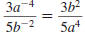
Here, x ≠0 and y ≠0.
A fraction raised to a negative exponent may be
rewritten as the
reciprocal of the fraction raised to the corresponding positive
exponent.
Property
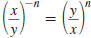
Example 1
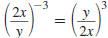
Example 2
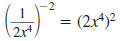
Here, x ≠0 and y ≠0. |
Example 8.2.5
Simplify and write using only positive exponents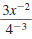
Solution
Use this property: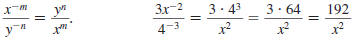
Example 8.2.6
Simplify and write using only positive exponents: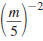
Solution
Use this property: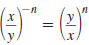 |
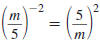 |
| Use the Power of a Quotient Property. |
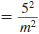 |
| Simplify. |
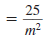 |
To rewrite a fraction raised to a negative
power, just “flip” the fraction and change
the negative power to positive
There’s more than one way to simplify the
original expression. For example, you
could begin like this:
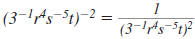
Then use the Power of a Product Property.
The national debt is continually changing,
minute by minute, day by day.
Simplifying Expressions That Contain Negative
Exponents
When we write an exponential expression in simplified form, we typically
use only positive exponents.
Example 8.2.7
Simplify and write using only positive exponents: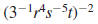
Solution
| Use the Power of a Product Property. |
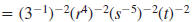 |
| Use the Power of a Power Property. |
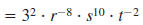 |
| Rewrite using only positive exponents. |
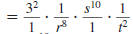 |
| Simplify. |
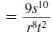 |
So,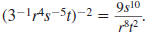
Example 8.2.8
Simplify and write using only positive exponents:
Solution
For each factor with a negative exponent, move
the factor to the other side of the division bar
and make its exponent positive. |
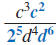 |
| Use the Multiplication Property of Exponents. |
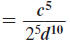 |
| Evaluate 25. |
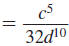 |
So,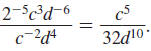
Scientific Notation
It is often difficult to read and work with very large or very small numbers.
For example,
• In mid-2002, the U. S. national debt was approximately
$5,600,000,000,000. To calculate the amount of money owed by each
American, we would divide this number by the U. S. population.
Unfortunately, 5600000000000 will not fit in the display of most
calculators.
• The rest mass of an electron is about
0.000000000000000000000000000000911 kilograms. It is very
difficult to work with a number that has so many zeros.
Numbers such as 0.000000000000000000000000000000911 and
5,600,000,000,000 are said to be written in expanded form.
To make it easier to read and work with very large or very small numbers,
we often use scientific notation.
For example, 2.1 ×105 is written in scientific notation.
In expanded form we write,
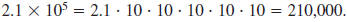
— Definition —
Scientific Notation
A number is written in scientific notation when it has the form
N ×10n
where 1 ≤N <10, N is written in decimal notation,
and n is an integer. |
Here’s how to convert a number from expanded form to
scientific notation.
Procedure —
To Convert From Expanded Form to Scientific Notation
Step 1 Move the decimal point until there is only one nonzero
digit
to its left.
Step 2 Write the number from Step 1 multiplied by a power of 10.
To find the power, count the number of places you moved
the decimal point.
• If you moved the decimal point to the left, the power is
positive.
• If you moved the decimal point to the right, the power is
negative.
Step 3 Check the sign of the power.
• If the original number was greater than or equal to 10,
the power should be positive.
• If the original number was greater than 0 and less than 1,
the power should be negative. |
The term “rest mass” means the mass
when the electron is not moving. As an
electron moves faster, its mass increases
(according to Einstein’s Theory of Special
Relativity).
Remember, you can write a whole number
using a decimal point.
For example: 239 =239.0
Example 8.2.9
The distance from the sun to the earth is approximately
93,000,000 miles.
Write 93,000,000 in scientific notation.
Solution
Step 1 Move the decimal point until there is
only one nonzero digit to its left.
The original number is not written with a 93,000,000
decimal point.
Since the number is a whole number, we
can rewrite it with a decimal point to the =93,000,000.
right of the last digit.
Then we move that decimal point seven 
places to the left.
Step 2 Write the number from Step 1
multiplied by a power of 10.
We moved the decimal point 7 places to the left.
So the power of 10 is 7. =9.3 ×107
Step 3 Check the sign of the power.
The original number is greater than 10, so the power should be
positive,
and it is.
We can also check our result by expanding 9.3 ×107.
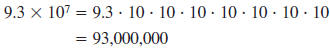
Thus, 93,000,000 miles =9.3 ×107 miles.
Example 8.2.10
The rest mass of an electron is approximately
0.000000000000000000000000000000911 kg.
Write this number in scientific notation.
Solution
Step 1 Move the decimal point until there is
only one nonzero digit to its left.
Move the decimal point until it is between the 9 and the 1.

Step 2 Write the number from Step 1
multiplied by a power of 10.
We moved the decimal point 31 places to the right.
So the power of 10 is -31. 9.11× 10-31
Step 3 Check the sign of the power.
The original number is less than1, so the power should be negative,
and it is.
Thus,
0.000000000000000000000000000000911 kg = 9.11× 10-31 kg.
We can also convert a number from scientific notation to expanded form.
— Procedure —
To Convert From Scientific Notation to Expanded Form
Move the decimal point the same number of places as the exponent
of 10.
• If the exponent is positive, move the decimal point right.
• If the exponent is negative, move the decimal point left.
As a check, note the following:
• If the power of 10 is positive, the number written in expanded
form will be greater than or equal to 10.
• If the power of 10 is negative, the number written in expanded
form will be greater than 0 and less than 1. |
Example 8.2.11
A light year is a measure of distance.
Its value is approximately 5.87× 1012 miles.
Write in expanded form: 5.87 ×1012
Solution
The exponent, 12, is positive, so move the
decimal point 12 places to the right.
As you move the decimal point, you will have
to append zeros to the right of 587 to serve as
place holders.

The result is: 5,870,000,000,000
A light year is almost 6 trillion miles
Be careful! The power of 10 does NOT tell
us how many zeros to append to the right
of the number.
To write 5.87×1012 in expanded form,
we append 10 zeros (not 12).
In 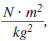 the abbreviations
are: the abbreviations
are:
N for Newton, a unit of force
m for meter, a unit of length
kg for kilogram, a unit of mass.
Example 8.2.12
The gravitational force of attraction between two masses,
m1 and m2,
that are a distance r apart is given by 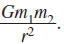
The G in the formula represents the universal gravitational constant,
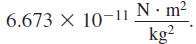
Write 6.673 ×10 -11 in expanded form.
Solution
The exponent, 11, is negative, so move the decimal point 11 places to
the left.
As you move the decimal point, you will have to append zeros to the left
of 6673 to serve as place holders.
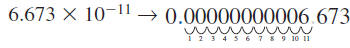
Thus,
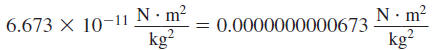
Here is a summary of this concept from Interactive
Mathematics.

CONCEPT 2:
MULTIPLYING AND DIVIDING
RATIONAL EXPRESSIONS
CONTAINING BINOMIALS
| Reducing Rational Expressions of the Form |
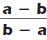 |
Sometimes we need to simplify an expression such
as the following: |
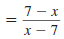 |
In the expression, notice that the numerator and
denominator are the same except for the signs of
the terms. |
|
To reduce the expression, we first factor -1
out of the numerator. |
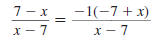 |
| Then we cancel common factors. |
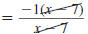 |
| The result is -1. |
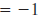 |
— Formula —
To Simplify a Rational Expression of the Form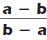
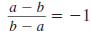
Here, a and b are real numbers and a≠ b. |
Example 8.2.13
Reduce to lowest term: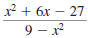
Solution
Step 1 Factor the numerator and denominator.
For the numerator, find two numbers whose
product is -27 and whose sum is 6. These
numbers are -3 and 9. |
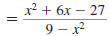 |
The denominator is the difference of two
squares: 32 -x2. |
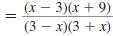 |
Step 2 Cancel all pairs of factors common to the
numerator and denominator.
Since
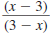 has the form has the form
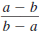 , it reduces to -1. , it reduces to -1.
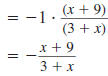
Thus,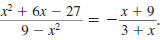
Concept 2 has sections on
• Reducing Rational
Expressions of the Form
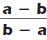
• Multiplying Rational
Expressions
• Dividing Rational
Expressions
• Simplifying a Complex
Fraction
Notice that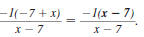
The answer may be written in several
ways.
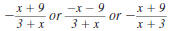
Here is an example of multiplying rational
expressions that contain monomials:
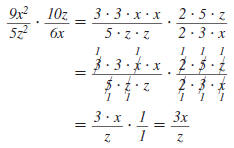
Multiplying Rational Expressions
In Lesson 8.1 you multiplied rational expressions that contain monomials.
Now, we will use the same procedure to multiply rational expressions that
contain binomials or trinomials.
— Procedure —
To Multiply Rational Expressions
Step 1 Factor the numerators and denominators.
Step 2 Cancel all pairs of factors common to the numerators and
denominators.
Step 3 Multiply the numerators. Multiply the denominators.
We usually leave the answer in factored form. |
Example 8.2.14
Find: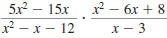
| Solution |
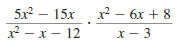 |
Step 1 Factor the numerators and
denominators. |
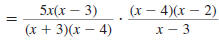 |
Step 2 Cancel all pairs of factors
common to the numerators
and denominators. |
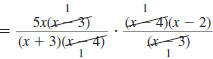 |
Step 3 Multiply the numerators,
and then multiply the
denominators. |
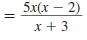 |
Thus,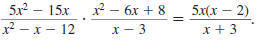
Example 8.2.15
Find: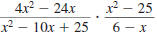
| Solution |
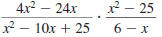 |
Step 1 Factor the numerators and
denominators. |
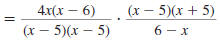 |
Step 2 Cancel all pairs of factors
common to the numerators
and denominators. |
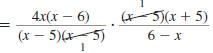 |
Replace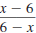 with-1 with-1 |
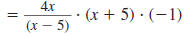 |
Step 3 Multiply the numerators,
and then multiply the
denominators. |
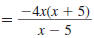 |
so,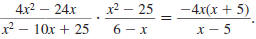
Dividing Rational Expressions
In Lesson 8.1 you divided rational expressions containing monomials.
Now, we will use the same procedure to divide rational expressions that
contain binomials or trinomials.
— Procedure —
To Divide Rational Expressions
Step 1 Invert the second fraction and change the division symbol,
÷, to the multiplication symbol, .
Step 2 Factor the numerators and denominators.
Step 3 Cancel all pairs of factors common to the numerators and
denominators.
Step 4 Multiply the numerators. Multiply the denominators.
We usually leave the answer in factored form. |
Example 8.2.16
Find: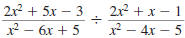
| Solution |
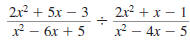 |
Step 1 Invert the second fraction
and change the division
symbol,÷ , to the
multiplication symbol, . |
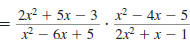 |
Step 2 Factor the numerators
and denominators. |
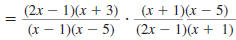 |
Step 3 Cancel all pairs of factors
common to the numerators
and denominators. |
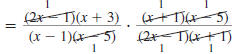 |
Step 4 Multiply the numerators.
Multiply the denominators. |
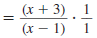 |
Step 4 Multiply the numerators.
Multiply the denominators. |
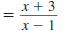 |
Thus, 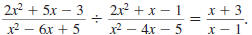
Here is an example of dividing rational
expressions that contain monomials:
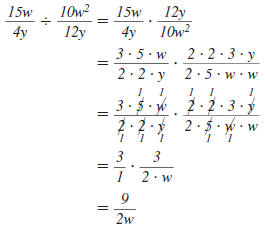
You can also write the answer as follows:
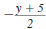
Example 8.2.17
Find: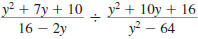
| Solution |
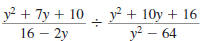 |
Step 1 Invert the second fraction
and change the division
symbol,÷ , to the
multiplication symbol, . |
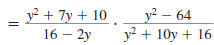 |
Step 2 Factor the numerators and
denominators |
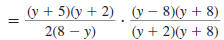 |
Step 3 Cancel all pairs of factors
common to the numerators
and denominators. |
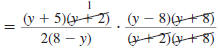 |
| |
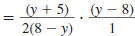 |
Replace 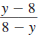 with
-1. with
-1. |
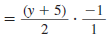 |
Step 4 Multiply the numerators.
Multiply the denominators. |
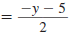 |
Thus,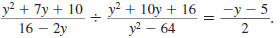
Simplifying a Complex Fraction
A complex fraction is a fraction that contains other fractions.
You have already used this procedure to simplify a complex fraction.
— Procedure —
To Simplify a Complex Fraction
Step 1 Write the complex fraction using a division symbol,÷ .
Step 2 Invert the second fraction and change the division symbol,
÷, to the multiplication symbol, .
Step 3 Factor the numerators and denominators.
Step 4 Cancel all pairs of factors common to the numerators and
denominators.
Step 5 Multiply the numerators. Multiply the denominators. |
Example 8.2.18
Simplify: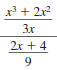
Solution
Step 1 Write the complex fraction
using a division symbol,÷ . |
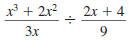 |
Step 2 Invert the second fraction
and change the division
symbol,÷ , to the
multiplication symbol, . |
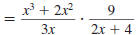 |
Step 3 Factor the numerators and
denominators. |
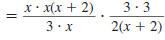 |
Step 4 Cancel all pairs of factors
common to the numerators
and denominators. |
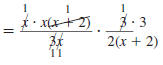 |
Step 5 Multiply the numerators.
Multiply the denominators. |
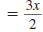 |
Thus,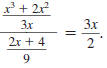
Example 8.2.19
Simplify:
Solution
Step 1 Write the complex fraction
using a division symbol,÷ . |
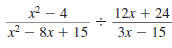 |
Step 2 Invert the second fraction
and change the division
symbol,÷ , to the
multiplication symbol, |
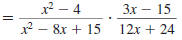 |
Step 3 Factor the numerators
and denominators |
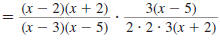 |
Step 4 Cancel all pairs of factors
common to the numerators
and denominators. |
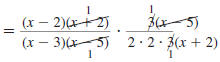 |
Step 5 Multiply the numerators.
Multiply the denominators. |
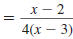 |
Thus,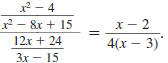
Here is a summary of this concept from Interactive
Mathematics

Concept 3 has sections on
• Finding the Least Common
Multiple (LCM) of a Set of
Polynomials
• Adding and Subtracting
Rational Expressions with
Different Denominators
• Simplifying a Complex
Fraction that Contains
Addition or Subtraction
CONCEPT 3:
ADDING AND SUBTRACTING
RATIONAL EXPRESSIONS
CONTAINING BINOMIALS
Finding the Least Common Multiple (LCM)
of a Set of Polynomials
Adding and subtracting rational expressions with different denominators is
like adding and subtracting fractions with different denominators.
We begin by finding the least common denominator (LCD) of a set of
rational expressions.
The LCD of two or more rational expressions is the least common
multiple (LCM) of their denominators.
We can find the LCM of a set of polynomials in much the
same manner
that we found the LCM of a set of whole numbers.
— Procedure —
To Find the Least Common Multiple (LCM) of a Set of Polynomials
Step 1 Factor each polynomial.
Step 2 For each factor, list it the greatest number of times it
appears
in any factorization.
Step 3 Find the product of the factors in the list.
We usually leave the LCM in factored form. |
Example 8.2.20
Find the LCM of 15xy, 10x2y, and 6xy2.
Solution
Step 1 Factor each polynomial.
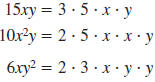
Step 2 For each factor, list it the
greatest number of times
it appears in any factorization.
2, 3, 5, x, x, y, y
Step 3 Find the product of the factors
in the list.
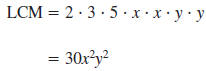
The LCM of 15xy, 10x2y, and 6xy2 is
30x2y2.
Example 8.2.21
Find the LCM of 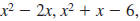 and and
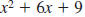
Solution
Step 1 Factor each polynomial.
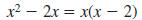
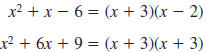
Step 2 For each factor, list it
the greatest number of
times it appears in any
factorization
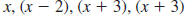
Step 3 Find the product of the
factors in the list
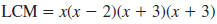
The LCM of 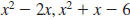 , and , and
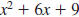 is is 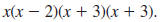
To find the LCM of a set of numbers, say
10, 15, and 18, follow these steps:
Step 1 Write the prime factorization of
each number.
10= 2· 5
15 =3 ·5
18 =2· 3 ·3
Step 2 List each prime factor the greatest
number of times it appears in any
factorization:
2, 3, 3, 5
Step 3 Multiply the prime factors in the
list:
2 ·3· 3· 5 =90
The LCM of 10, 15, and 18 is 90.
To add (or subtract) fractions with
different denominators, say
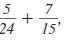
follow these steps:
Step 1 Find the LCD.
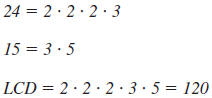
Step 2 Rewrite each fraction with the LCD
as the denominator
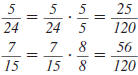
Step 3 Add (or subtract) the numerators.
The denominator stays the same.
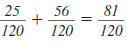
Step 4 Reduce to lowest terms.
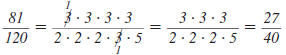
Adding and Subtracting Rational Expressions with
Different Denominators
We add or subtract rational expressions in the same way that we add or
subtract fractions.
You have already learned how to add and subtract rational expressions
with the same denominator. Now we will add and subtract rational
expressions with different denominators.
— Procedure —
To Add (or Subtract) Rational
Expressions That Have Different Denominators
Step 1 Find the LCD.
Step 2 Rewrite each rational expression with the LCD as the
denominator.
Step 3 Add (or subtract) the numerators.
The denominator stays the same.
Step 4 Reduce to lowest terms.
We usually leave the answer in factored form. |
Example 8.2.22
Find: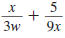
Solution
| Step 1 Find the LCD. |
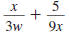 |
| Factor each denominator. |
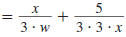 |
List each factor the greatest number
of times it appears in any factorization.
The LCD is 3·3 ·w· x =9wx |
3, 3, w, x |
Step 2 Rewrite each rational
expression with the LCD
as the denominator. |
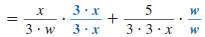 |
| |
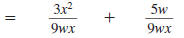 |
Step 3 Add (or subtract) the
numerators. The
denominator stays the
same. |
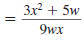 |
Step 4 Reduce to lowest terms.
The numerator and denominator have no
common factors other than 1 and 1.
Therefore,
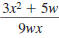 5w is in lowest terms. 5w is in lowest terms.
Thus,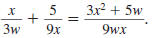
Example 8.2.23
Find: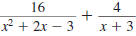
Solution
Step 1 Find the LCD.
Factor each denominator.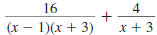
The LCD is (x- 1)(x -3).
Step 2 Rewrite each rational expression
with the LCD as the denominator.
The denominator of the first
fraction is already the LCD.
The denominator of the second
fraction needs another factor,
(x -1).
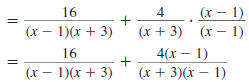
Step 3 Add (or subtract) the numerators.
The denominator stays the same.
| Add the numerators. |
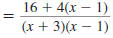 |
| Distribute the 4 |
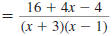 |
| Combine like terms. |
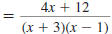 |
Step 4 Reduce to lowest terms.
Factor the numerator. |
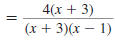 |
Cancel the common factor,
(x +3). |
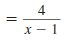 |
So,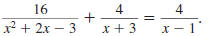
At the end of Step 2, you may be tempted to
cancel common factors.
But that would get you back to where you
started.
Remember to add first, then factor and
cancel factors
At the end of Step 2, you may be tempted to
cancel common factors.
But that would get you back to where you
started.
Remember to subtract first, then factor and
cancel factors.
Example 8.2.24
Find: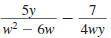
Solution
Step 1 Find the LCD.
Factor each denominator.
The LCD is w (w -6) ·2· 2· y.
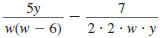
Step 2 Rewrite each
rational expression
with the LCD as
the denominator
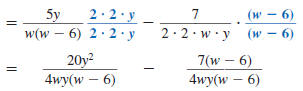
Step 3 Add (or subtract) the numerators.
The denominator stays the same.
| Subtract the numerators |
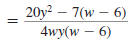 |
| Distribute the -7. |
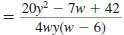 |
Step 4 Reduce to lowest terms.
The numerator cannot be factored using integers. Since there are no
factors, other than 1 or -1, common to the numerator and denominator,
the expression is in lowest terms.
So,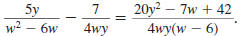
Example 8.2.25
Find: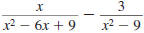
Solution
Step 1 Find the LCD.
Factor each denominator.
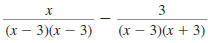
The LCD is (x -3)(x- 3)(x -3).
Step 2 Rewrite each rational expression
with the LCD as the denominator
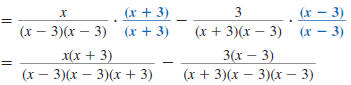
Step 3 Add (or subtract) the numerators. The
denominator stays the
same.
| Subtract the numerators. |
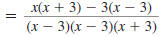 |
In the numerator,
distribute the x and the -3. |
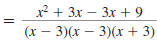 |
| Combine like terms. |
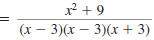 |
Step 4 Reduce to lowest terms.
The numerator cannot be factored over the integers.
Since there are no factors, other than 1 or -1, common to the numerator
and the denominator, the expression is in lowest terms.
So,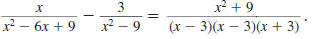
Simplifying a Complex Fraction That Contains
Addition or Subtraction
You have already simplified some complex fractions. Now we will learn
how to simplify a complex fraction that contains addition or subtraction.
One way to begin is to carry out the addition or subtraction.
— Procedure —
To Simplify a Complex Fraction
That Contains Addition or Subtraction.
Step 1 Perform any addition or subtraction.
Step 2 Rewrite the complex fraction using a division symbol, ÷.
Step 3 Invert the second fraction and change the division symbol,
÷, to the multiplication symbol, .
Step 4 Factor the numerators and denominators.
Step 5 Cancel all pairs of factors common to the numerators and
denominators.
Step 6 Multiply the numerators. Multiply the denominators. |
Example 8.2.26
Simplify: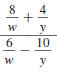
Solution
Step 1 Perform any addition or subtraction.
In both the numerator and denominator
the LCD of the fractions is w y. |
|
| We write each fraction with LCD. |
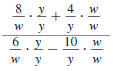 |
Then we add the fractions in the
numerator and subtract the fractions
in the denominator. |
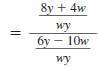 |
Step 2 Rewrite the complex fraction
using a division symbol,÷. |
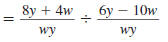 |
Step 3 Invert the second fraction and
change the division symbol, ÷,
to the multiplication symbol, . |
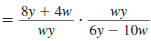 |
Step 4 Factor the numerators and
denominators. |
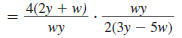 |
Step 5 Cancel all pairs of factors
common to the numerators
and denominators. |
|
| The common factors are 2, w, and y. |
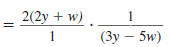 |
Step 6 Multiply the numerators.
Multiply the denominators. |
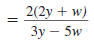 |
Thus,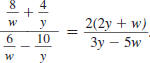
Example 8.2.27
Simplify: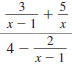
Solution
Step 1 Perform any addition or subtraction.
In the numerator, the LCD of the
fractions is x (x -1). |
|
In the denominator, the LCD of the
fractions is x -1. |
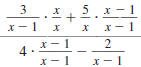 |
Add the fractions in the numerator.
Subtract the fractions in the
denominator. |
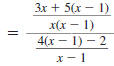 |
Distribute the 5 in the numerator of
the complex fraction. |
|
Distribute the 4 in the denominator
of the complex fraction. |
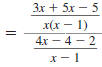 |
| Combine like terms. |
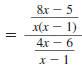 |
Step 2 Rewrite the complex fraction
using a division symbol, ÷. |
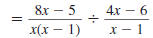 |
Step 3 Invert the second fraction and
change the division symbol,÷ ,
to the multiplication symbol, |
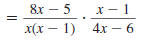 |
Step 4 Factor the numerators and
denominators. |
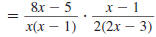 |
Step 5 Cancel all pairs of factors
common to the numerators
and denominators. |
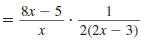 |
| Cancel the common factor, x 1. |
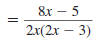 |
Step 6 Multiply the numerators.
Multiply the denominators. |
|
Thus,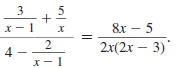
Here is a summary of this concept from Interactive
Mathematics.

Checklist Lesson 8.2
|


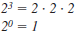
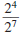
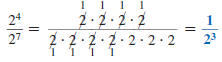
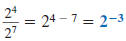
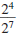 simplifies to
both
simplifies to
both 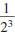 and
and 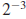 ,
we conclude
,
we conclude 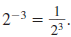
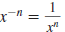
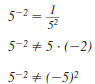
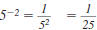 positive
positive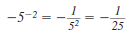 negative
negative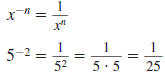
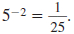
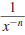 , as follows:
, as follows: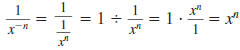
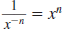
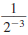
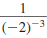
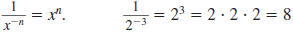
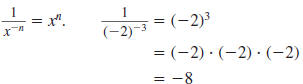
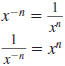
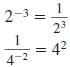
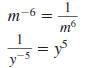
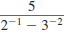
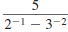
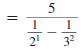
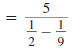
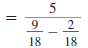
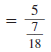
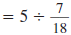
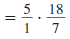
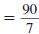
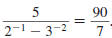
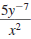
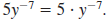
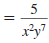
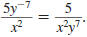
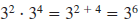
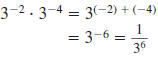
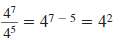
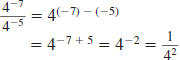
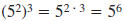
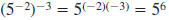
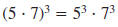
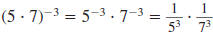
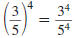
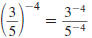
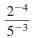 .
.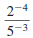
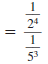
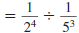
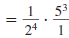
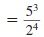
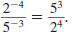
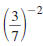 .
.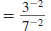
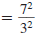
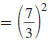
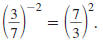
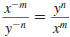
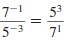
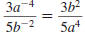
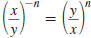
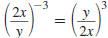
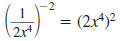
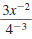
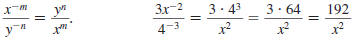
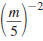
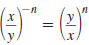
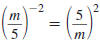
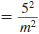
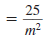
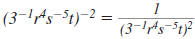
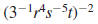
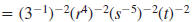
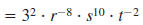
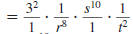
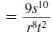
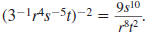
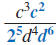
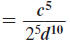
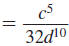
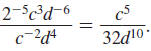
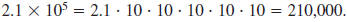

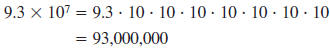


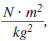 the abbreviations
are:
the abbreviations
are: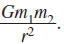
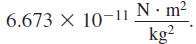
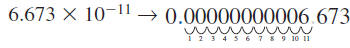
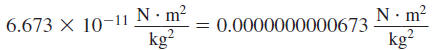

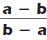
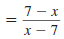
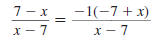
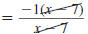
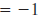
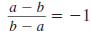
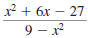
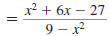
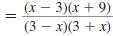
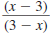 has the form
has the form
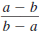 , it reduces to -1.
, it reduces to -1.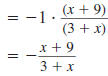
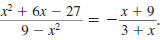
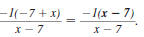
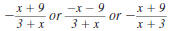
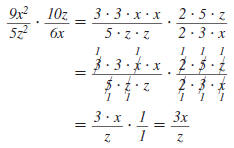
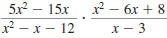
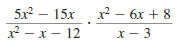
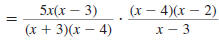
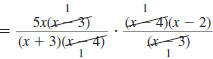
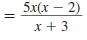
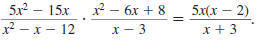
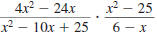
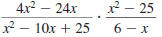
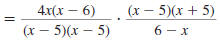
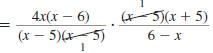
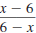 with-1
with-1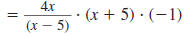
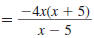
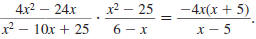
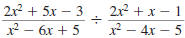
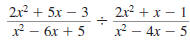
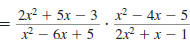
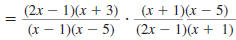
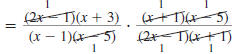
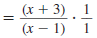
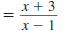
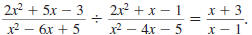
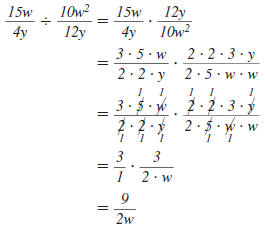
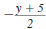
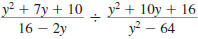
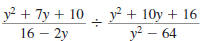
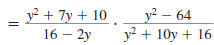
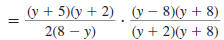
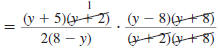
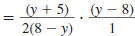
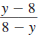 with
-1.
with
-1.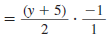
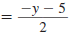
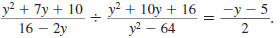
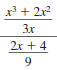
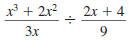
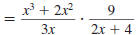
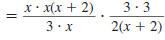
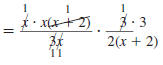
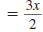
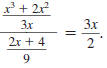
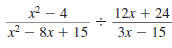
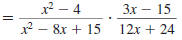
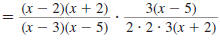
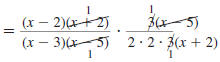
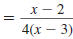
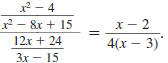

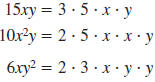
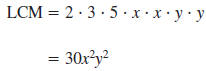
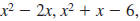 and
and
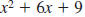
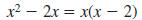
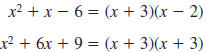
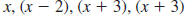
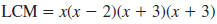
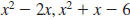 , and
, and
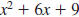 is
is 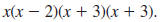
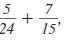
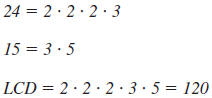
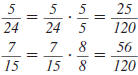
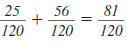
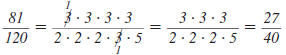
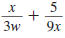
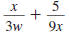
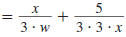
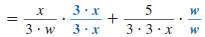
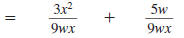
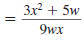
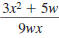 5w is in lowest terms.
5w is in lowest terms.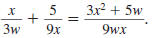
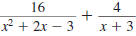
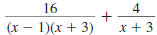
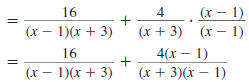
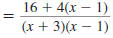
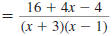
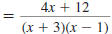
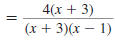
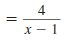
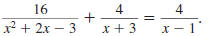
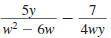
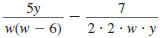
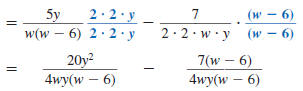
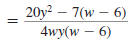
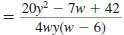
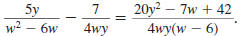
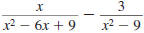
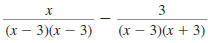
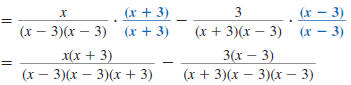
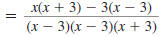
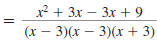
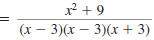
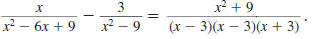
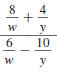
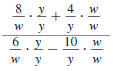
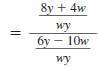
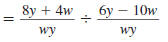
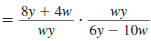
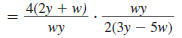
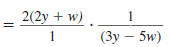
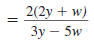
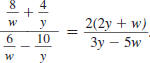
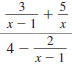
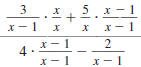
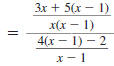
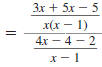
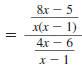
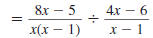
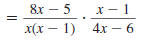
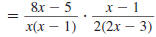
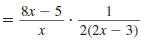
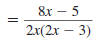
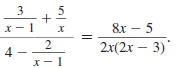

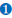 Negative
Exponent
Negative
Exponent
 Properties
of Negative Exponents
Properties
of Negative Exponents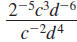
 Scientific
Notation
Scientific
Notation Reduce a
Rational Expression of the Form
Reduce a
Rational Expression of the Form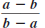
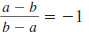
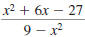
 Multiply
Rational Expressions
Multiply
Rational Expressions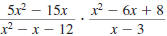
 Divide
Rational Expressions
Divide
Rational Expressions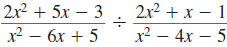
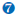 Complex
Fractions
Complex
Fractions
 Least
Common Multiple (LCM)
Least
Common Multiple (LCM)