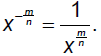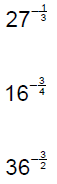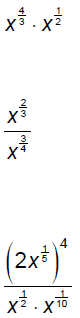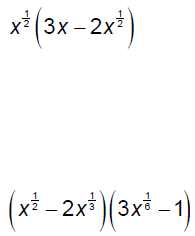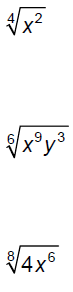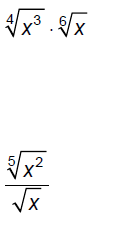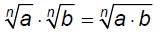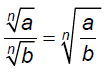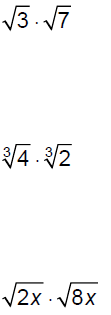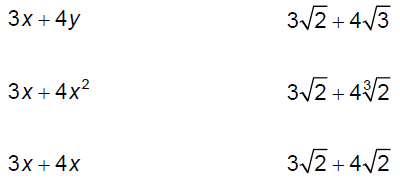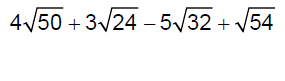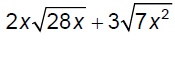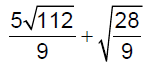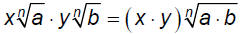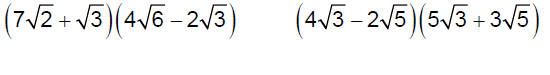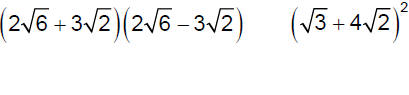|
Home |
Radical Expressions & Radical FunctionsWhat is a square root of 25? How many square roots does 25 have? Definition: X is a square root of a if X² = a. Symbolically,
Do the following square roots exist?
What are the following square roots?
In general…. A square root is a particular type of root that uses the root sign for
In the above expression, the 64z^4 is the radicand. The radicand is f (x) =
Definition: A number S is called a perfect square if it’s the result of You need to memorize the first 21 numeric perfect squares.
Variable expressions can be perfect squares An expression is a perfect square if its The square root of a numeric value that isn’t a perfect square Recall that irrational numbers cannot be expressed as fractions of Definition: X is a cube root of a if X³ = a.
All numbers have one cube root thus every cube root is a principle
Definition: A number C is called a perfect cube if it’s the result of You need to memorize the first 11 numeric perfect cubes.
Variable expressions can be perfect cubes An expression is a perfect cube if its Definitions: X is a fourth root of a if X4 = a. All roots have an index. The index of a root is equal to
the power Roots with an even index (such as square roots and fourth
roots)… Roots with an odd index (such as cube roots and fifth
roots)… Notationally write the fourth roots of 81 and evaluate. Notationally write the fifth root of 243 and evaluate. Definitions: A number R is called a perfect fourth if it’s
the result of
For roots with even indices, keep in mind the following rule: If variables can represent any real number, you may need
to use absolute If the variables can only represent non‐negative numbers,
you won’t need Absolute value symbols are never needed if a root has an odd index. Find each root. Assume that all variables represent
non‐negative
Find each root. Assume that all variables can represent
any real
§10.2 Radicals and Rational ExponentsRecall the Laws of Exponents (x ≥ 0)
Also:
Think about how the Laws of Exponents are related here:
Explore the possibilities associated with the following
rational
Thus in general we can conclude that
Evaluate and/or simplify.
Rewrite each expression in radical notation and simplify as possible.
Recall that Evaluate.
Use the properties of exponents to simplify each
expression.
Multiply.
Factor.
Use rational exponents with each to find a single simplified radical.
Use rational exponents with each to find a single simplified radical.
§10.3 Product & Quotient Rules and Simplifying Radical ExpressionsProduct Rule for Radicals:
Quotient Rule for Radicals:
Multiply.
Divide.
To simplify radicals, apply the product and quotient rules
in reverse.
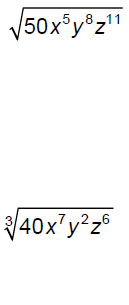
Simplify.
Simplify .
Emphasis: its all about perfect squares, cubes, etc.
Simplify.
Simplify.
Simplify.
§10.4 Adding, Subtracting, and further Multiplying RadicalsCompare the following pairs of sums
To add or subtract radicals, you must have like radicals. Add.
Subtract.
Add and/or subtract.
Add.
Add.
To multiply radicals with coefficients, keep the following
rule in
Multiply.
Multiply.
Multiply.
|
||||||||||||||


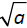 is the principle square root of a. To symbolically
is the principle square root of a. To symbolically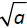 and −
and −
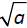 .
This
.
This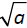 .
.

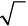 is called a “radical sign” or a “root sign”.
is called a “radical sign” or a “root sign”. is an example of a radical expression since it an expression
is an example of a radical expression since it an expression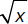 is an example of a radical function.
is an example of a radical function.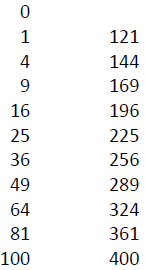
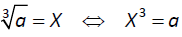

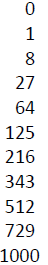
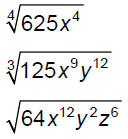
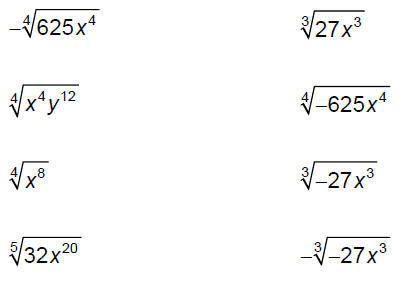
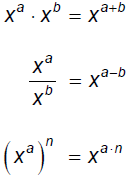
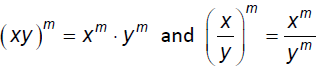

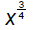
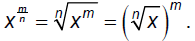
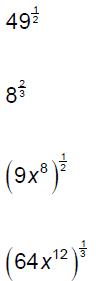
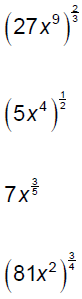
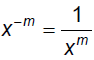 which we
can extend to define
which we
can extend to define