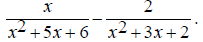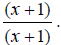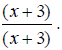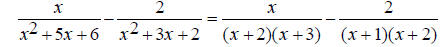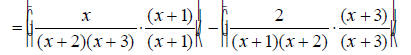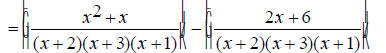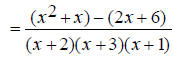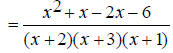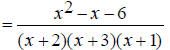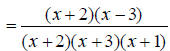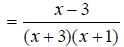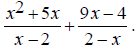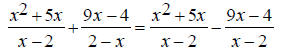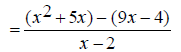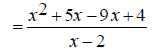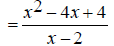|
Home |
Rational Expressions and Common DenominatorsIn order to perform addition and subtraction operations
with rational numbers, it is necessary to convert all For example, the operation
To add or subtract rational numbers or expressions, you
must have a common denominator. Once both terms A common denominator is generally chosen to be the
least common multiple of the denominators. For rational EX: Find the least common multiple of 16 and 40. The standard way for finding the least common multiple of
two integers involves computing the prime 16 = 2 * 2* 2 * 2 and 40 = 2 * 2* 2 * 5 It may be helpful to list the factors in a table form in
order to carry out the process. We also include a
The next step is to move all factors that are common to
both 16 and 40 over to the least common
Now move over all remaining factors of the first number.
And then the remaining factors of the second number.
Finally, multiply out all of the least common multiple
factors. The least common multiple is therefore EX: Find the least common multiple of 30, 24, and 32. Finding the least common multiple of three integers is
slightly more complicated, but the process is very
First move over all factors that are common to all three. In this case, a single 2 is the only one.
Then move over all factors that are common to the first and second numbers. Only a single 3 qualifies.
Move over all factors common to the first and third. There are none. Next move over all factors common to the second and third. Only a single 2 qualifies.
Go in order, moving over the remaining factors from each of the three numbers.
Finally, multiply the factors out to get the least common multiple: 2 * 3* 2* 5* 3* 2 * 2 * 2 = 2* 2 * 2 * 2 * 2* 3* 3* 5 = 1440 Thus the least common multiple is 1440. Notice that the factorization of the least common multiple
completely contains the factorization of each EX: Find the least common multiple of
For expressions with variables and exponents, it is very
simple to find the least common multiple. For For x, the highest exponent is 5, in the second
expression. Therefore the least common multiple is
EX: Find the least common multiple of x^2 + 5x + 6 and x^2 - 9 . Just like with integers, the first step towards finding a
least common multiple of polynomials is to factor
Move the common factors over. In this case, only (x + 3) is common.
Now move over the remaining factors from each expression.
Therefore the least common multiple of x^2 + 5x + 6 and x^2 - 9 is (x + 3)(x + 2)(x - 3) Adding Rational Expressions The following steps are necessary when adding rational expressions: 1) Find a common denominator. This is usually the least
common multiple of the denominators. EX: Simplify
The first step is to find the least common multiple of
(y^2)z and xy so that it can be used as a common Thus the common denominator will be x(y^2)z . Now find out what factors are missing from each
denominator that will make them equal to the common The first denominator is missing a single x, so multiply the first expression by x/x, which is equal to 1. The second denominator is missing yz , so multiply the
second expression by Now we get the following:
EX: Simplify
In this case, both addends have the same denominator.
Therefore the numerators can immediately be
[This cannot be further simplified.] EX: Simplify
Here we must first find the least common multiple of 6x and 8x.
The common factors are x and a single 2.
Move over the remaining factors for each.
Therefore the common denominator will be (2 * 2 * 2 * 3)x = 24x . Now find out what factors are missing from each
denominator that will make them equal to the common The first denominator is missing two 2's, so multiply the first expression by 4/4. The second denominator is missing a single 3, so multiply the second expression by 3/3. Now we get the following:
EX: Simplify
The denominators x +3 and x -2 are already completely
factored.
EX: Simplify
First find the least common multiple of the denominators. It is necessary to factor them first.
List these factors in table form.
Move over the common factors, in this only (x + 1) .
Move over the remaining factors from each term.
Therefore the least common multiple and common denominator
is x(x +1)(x - 1) .
Since 2x^2 + x -1 is of the form Ax^2 + Bx + C , where A ≠
0 , the middle term must be split.
Replace the numerator with its factored form.
Subtracting Rational Expressions Subtraction of rational expressions is done in the same
way as addition. The only difference is that all signs in EX: Simplify
In this case, both expressions have the same denominator.
Now just simplify the numerator
Both EX: Simplify
Find the common denominator. First factor the two denominators. x^2 + 5x + 6 = (x + 2)(x + 3) and x^2 + 3x + 2 = (x +1)(x + 2) The only common factor between the two denominators is (x
+ 2) , so the least common multiple and The first denominator is missing (x + 1) , so multiply the first expression by
The second denominator is missing (x + 3) , so multiply the second expression by
Some addition operations can turn into subtraction when the correct common denominator is found. EX: Simplify
Notice that the denominators, x - 2 and 2 - x are -1 multiples of each other ( 2 - x = -(x - 2) ). Because of this, we can change the second denominator to x
-2 and change the operation to
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 cannot be performed without converting to
cannot be performed without converting to
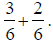
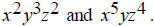
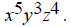
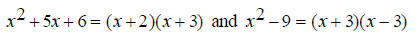
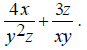
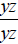 ,also equal to 1.
,also equal to 1.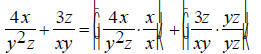
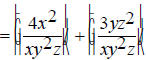
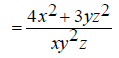
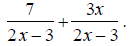
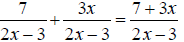
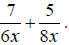
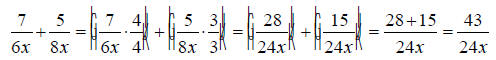
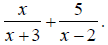
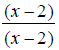 and the second term
by
and the second term
by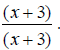
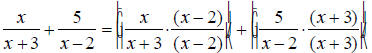
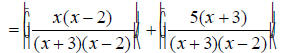
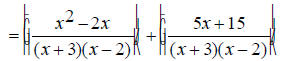
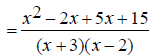
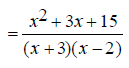
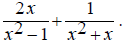
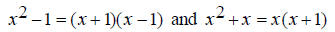
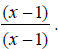
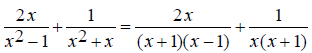
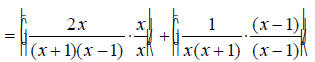
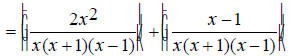
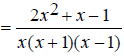
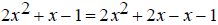
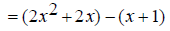
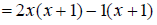
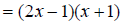
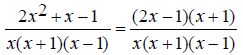
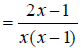
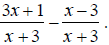
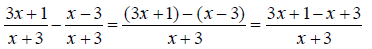
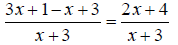
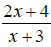 and
and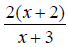 are
acceptable answers.
are
acceptable answers.