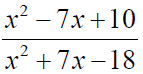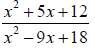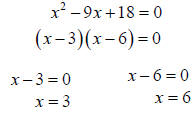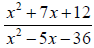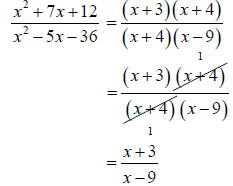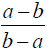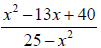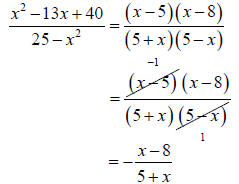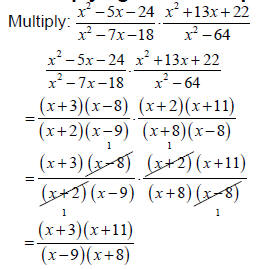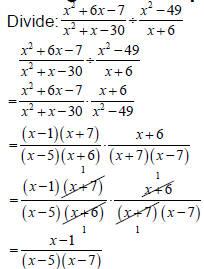Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Rational Expressions and Equations

Study Strategy –Preparing for a Cumulative Exam

•Preparing for a Cumulative Review
•Old Quizzes and Tests
•Homework and Notes
•Problems from Your Instructor
•Cumulative Review Exercises
•Applied Problems
•Study Groups

Section 7.1 –Rational Expressions and Functions

Concept –Rational Expressions
A rational expression is a quotient of two polynomials. The denominator of a rational expression must be nonzero, as division by zero is undefined.

Example –Rational Expressions

Concept –Values for Which a Rational Expression is Undefined

To find the values for which a rational expression is undefined, we set the denominator equal to 0 and solve the resulting equation. These solutions are the values for which the expression is undefined.

Example –Values for Which a Rational Expression is Undefined

Find the values for which the rational expression is undefined:

The expression is undefined for x=3,6.

Concept –Simplifying a Rational Expression to Lowest Terms

To simplify a rational expression to lowest terms, we first factor the numerator and denominator. Then we may divide out common factors in the numerator and denominator.

Example –Simplifying a Rational Expression to Lowest Terms

Simplify to lowest terms:

Concept –Factors That Are Opposites

Two expressions of the form a-b and b-a are opposites. The rational expression

simplifies to equal -1,as any fraction whose numerator is the opposite of its denominator is equal to -1.

Example –Factors That Are Opposites

Simplify to lowest terms:

Section 7.2 –Multiplication and Division of Rational Expressions

Concept –Multiplying Rational Expressions

To multiply two rational expressions, factor each numerator and denominator completely. Divide out factors that are common to a numerator and a denominator and multiply the remaining factors, leaving the numerator and denominator in factored form.

Example –Multiplying Rational Expressions

Concept –Dividing Rational Expressions

To divide a rational expression by another rational expression, replace the divisor by its reciprocal and then multiply.

Example –Dividing Rational Expressions