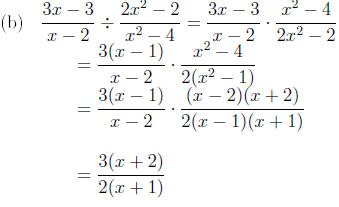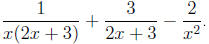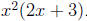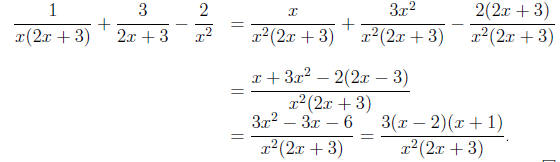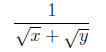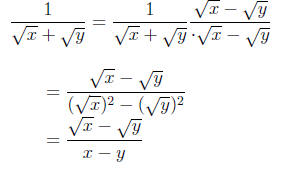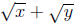Algebraic Expressions
Sets
Definition. A set is a collection of objects, and these objects are called the
elements of
the set.
If S is a set, then a ∈S means that a is an element of S, and
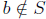 means that b is not means that b is not
an element of S.
Describing Sets
(1) Listing all its elements between curly brackets: S = {1, 2, 3, 4, 5}.
(2) If the elements of a set have a certain property, we can describe the set in
terms of
a generic variable that has that property.
Example. 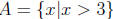 which
is read as A is the set of all x such that x is greater than 3 . which
is read as A is the set of all x such that x is greater than 3 .
Definitions
A variable is a letter that can represent any number from a given set of
numbers.
When variables such as x, y, and z and some real numbers, and combined using
addition,
subtraction, multiplication, division, powers, and roots, we obtain an algebraic
expression.
The domain of an algebraic expression is the set of all real numbers that might
represent
the variables (that is numbers for which denominators are not zero and roots
always exist).
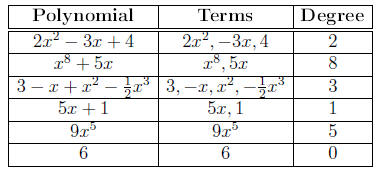
Definition A polynomial in the variable x is an
expression of the form
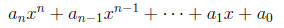
where 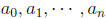 are real
numbers, and n is a nonnegative integer. If are real
numbers, and n is a nonnegative integer. If 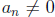 ,
then the ,
then the
polynomial has degree n. Note that the degree of a polynomial is the highest
power of the
variable that appears in the polynomial. The monomials
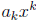 that make up the polynomial that make up the polynomial
are called the terms of the polynomial.
Example
Adding, Subtracting and Multiplying Polynomials
Examples Perform the indicated operations and simplify
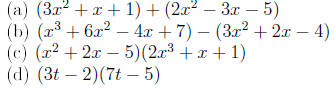
Solution. To obtain the sum of two polynomials in x we add
coefficients of like powers of x.
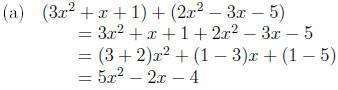 |
remove parentheses
add coefficients of like powers of x
simplify |
When multiplying two polynimials we use the distributive
properties.
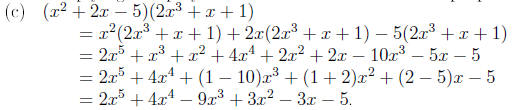
Product Formulas
If A and B are any real numbers or algebraic expressions, then
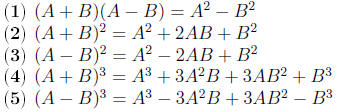
Examples Evaluate the expressions
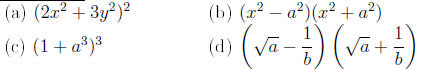
Solution.
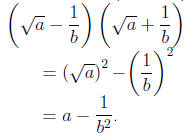
using product formula 1
Factoring Formulas
If A and B are any real numbers or algebraic expressions, then
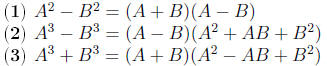
The first step in factoring expressions is to factor out
the common factors.
Example.
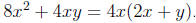
 1.4 Rational
Expressions 1.4 Rational
Expressions
Definition. A rational expression is the quotient
of two polynomials.
Examples Perform the indicated operation and simplify:
1. Products and quotients.

Solution.
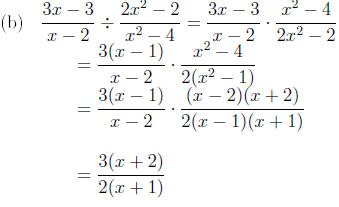 |
factoring out the factors 2 and 3
using the factoring formula 1
simplifying the factors x - 1 and x - 2 |
2. Sums and differences:
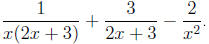
Solution. The denominators are already in factored form.
The lcd is 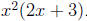
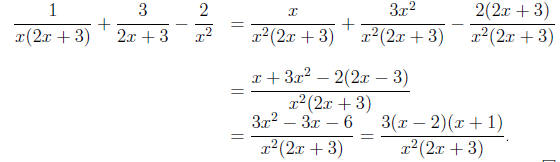
3. Rationalizing a denominator:
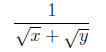
Solution.
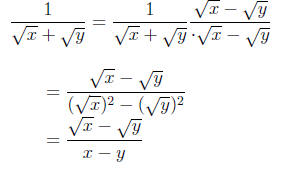 |
multiply the numerator and the
denominator by
the conjugate of
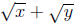 |
|


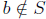 means that b is not
means that b is not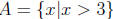 which
is read as A is the set of all x such that x is greater than 3 .
which
is read as A is the set of all x such that x is greater than 3 .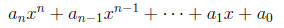
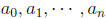 are real
numbers, and n is a nonnegative integer. If
are real
numbers, and n is a nonnegative integer. If 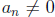 ,
then the
,
then the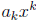 that make up the polynomial
that make up the polynomial
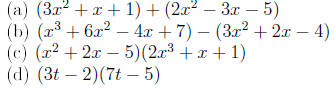
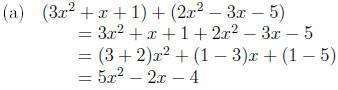
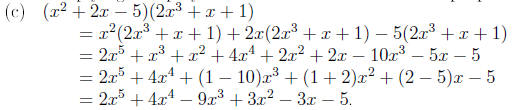
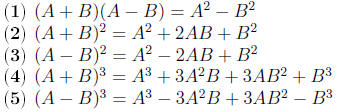
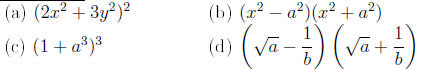
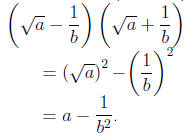
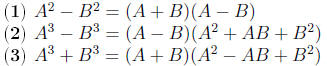
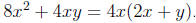
 1.4 Rational
Expressions
1.4 Rational
Expressions