|
|
Radical Expressions
Square Roots
Square Root
The number c is a square root of a if c2=a |
Ex. Find the roots of…
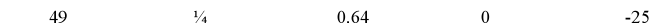
Principal Square Root
The principal square root of a nonnegative number is its nonnegative
square root.The symbol 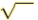 is called a
radical sign and is used to indicate the principal square root of the
number over which it appears is called a
radical sign and is used to indicate the principal square root of the
number over which it appears |
Ex. Find the principal root of…
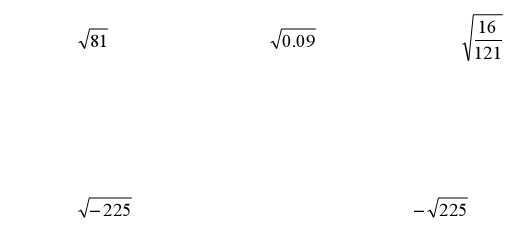
Properties of Square Roots
o Every positive real number has _________ real-numbered square roots
o The square root of zero is _________
o The square root of a negative number is _________ *
o The principal square root of a non-negative number is its _________
Graphs of radical functions and their domains
Ex. Graph f (x) =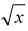 and find the domain and find the domain
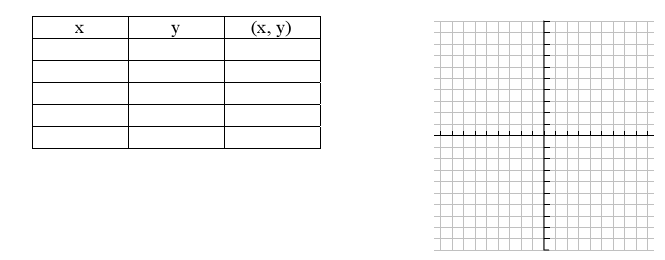
Ex. Graph g(x) =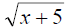 and find the domain and find the domain
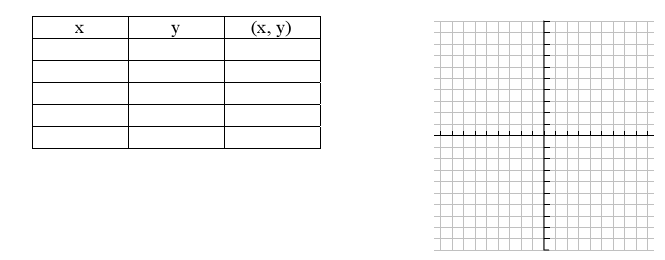
What is the principal square root of a2
Ex. Find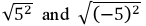
Simplifying 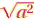
For any real number a ,
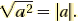
(The principal square root of a2 is the absolute value of a.) |
Ex. Find the principal square roots
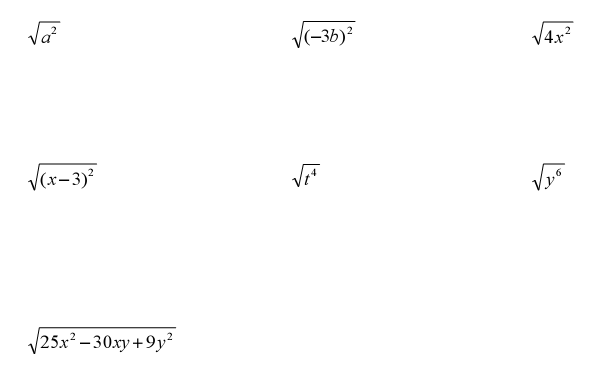
Cube Roots
Cube Root
The number c is the cube root of a if c3 =a.In symbols,we write
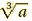 to denote the cube root of a. to denote the cube root of a. |
Ex. Find the cube roots of…

Ex. Graph f (x) =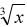 and find the domain and find the domain
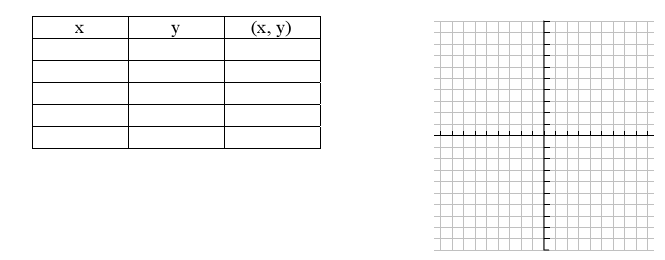
Ex. Simplifying the Cube Roots
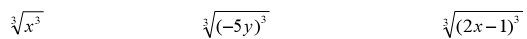
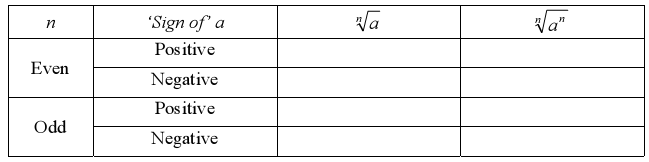
What are the nth roots?
• The fourth root of a number a is the number c for which c4 = a .There are
also 5th roots, 6th roots, and so on.
• We write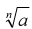 for the nth root. for the nth root.
• The number n is called the index (plural, indices). When the index is 2, we
do not write it.

Summary of Roots
Section 10.2 Rational Exponents
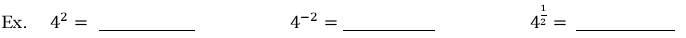
What are rational exponents?
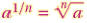
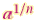 means means
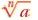 when a is nonnegative,n can be any
natural number greater 1.when a is negative ,n must be odd. when a is nonnegative,n can be any
natural number greater 1.when a is negative ,n must be odd. |

Positive Rational Exponents
For any natural numbers m and n(n≠1) and any real number a for which
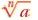 exists exists
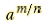 and and 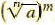 ,or ,or
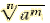 |
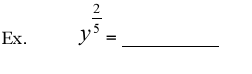
| Negative Rational Exponents
For any rational number m/n and any
nonzero real number a for which am/n exists
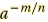 means means
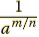 |
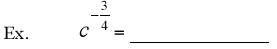
Radicals, Rational Exponents and Calculators
Ex. Approximate the following on your calculator. Round to 4 decimal places

Ex. Re-write each expression as a radical and evaluate
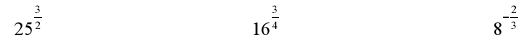
Laws of exponents
For any real numbers a and b and any rational exponents m and n for
which am,an and bm are defined |
1.am•an = am+n
2.am/an =am-n
3.(am)n=amn
4.(ab)m=ambm
|
In multiplying,add exponents if the bases are the same
In deviding,extract exponents if the bases are the same.(Assume a≠0.)
To raise a power to a power ,multiply the exponents
To raise a product to a power,raise each factor to the power and
multiply. |
Ex. Simplify…
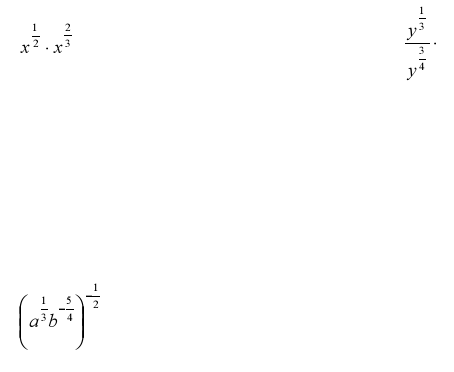
Ex. Use rational exponents to simplify … write as a radical, when appropriate
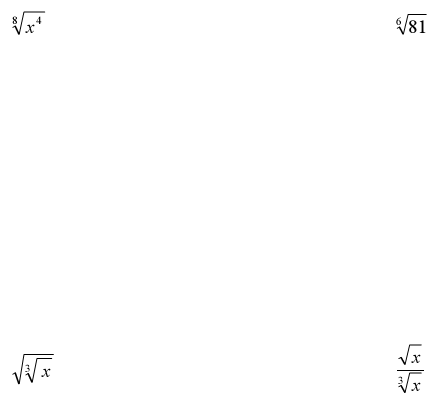
Section 10.3 Simplifying Radical Expressions
Multiplying and Simplifying Radical Expressions
The Product Rule for Radicals
For any real numbers 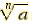 and and
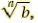
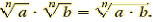
(The product of nth roots is the nth root of the product of the two
radicands) |
Ex. Multiply

Ex. Divide

Simplifying by factoring
To simplify a Radical expression with Index n by Factoring.
1.Express the radicand as a product in which one factor is the
largest perfect nth power possible .
2.Take the nth root of each factor.
3.Simplication is complete when no radicand has a factor that is a
perfect nth power. |
Ex. Simplify
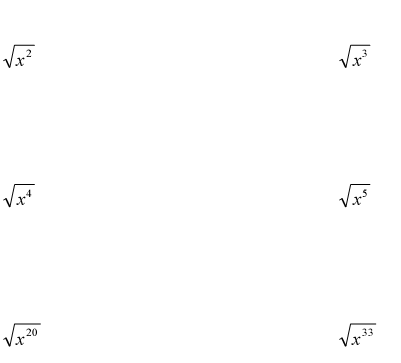

Ex. Simplify

Ex. Multiply and Simplify
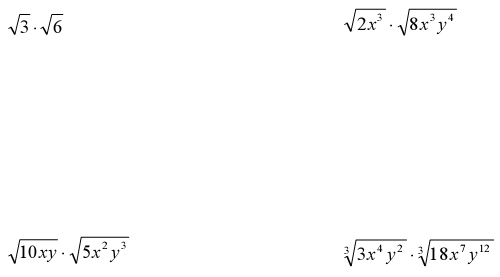
Section 10.4 Dividing Radicals and Rationalizing Denominators
The Quotient Rule for Radicand
For any real numbers 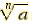 and and
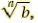 and b≠0 and b≠0
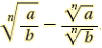 |
Rationalizing Denominators
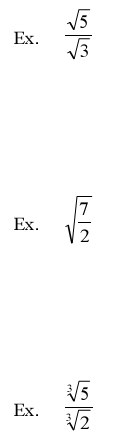
Section 10.5 Expressions Containing Several Radical Terms
Adding and Subtracting Radical Expressions
• Adding Radicals is very similar to adding polynomials – "combining like
radicals"
Ex. Simplify the radical expressions

More Multiplication and Division
• Use the Distributive Property, FOIL, etc…
Ex. Simplify the radical expressions
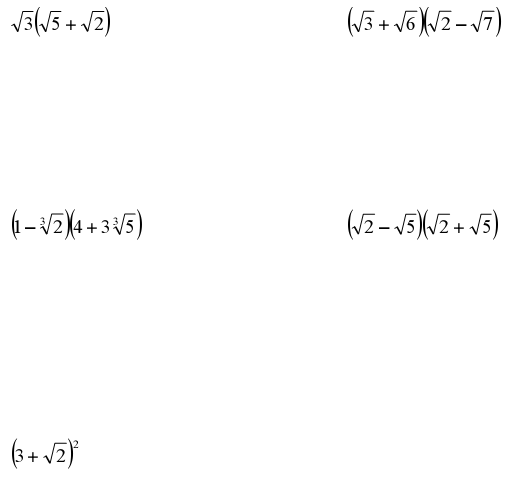
Section 10.8 Imaginary and Complex Numbers
| The number i i is the unique number for which i=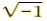 and
i2=-1 and
i2=-1 |
Ex. Find…

Powers of i
Ex. Find…

|


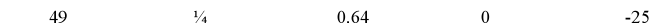
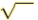 is called a
radical sign and is used to indicate the principal square root of the
number over which it appears
is called a
radical sign and is used to indicate the principal square root of the
number over which it appears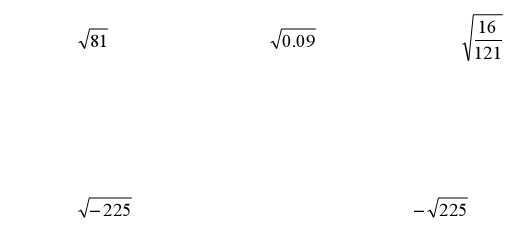
 and find the domain
and find the domain
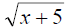 and find the domain
and find the domain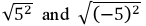
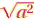
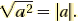
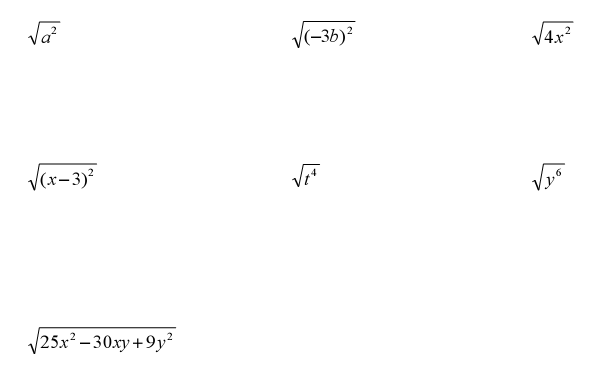
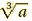 to denote the cube root of a.
to denote the cube root of a.
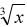 and find the domain
and find the domain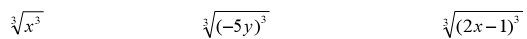
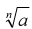 for the nth root.
for the nth root.

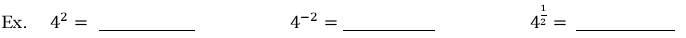
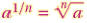
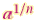 means
means
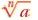 when a is nonnegative,n can be any
natural number greater 1.when a is negative ,n must be odd.
when a is nonnegative,n can be any
natural number greater 1.when a is negative ,n must be odd.
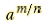 and
and 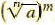 ,or
,or
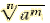
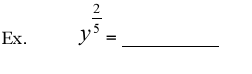
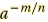 means
means
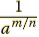
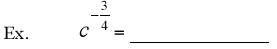

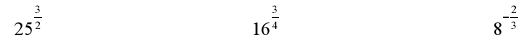
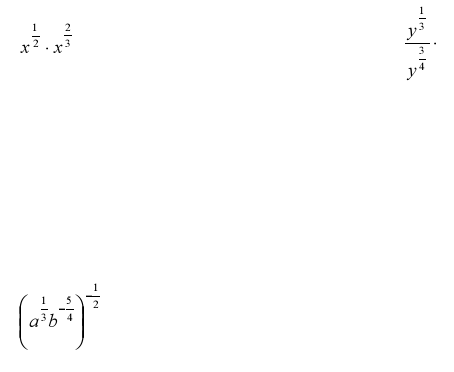
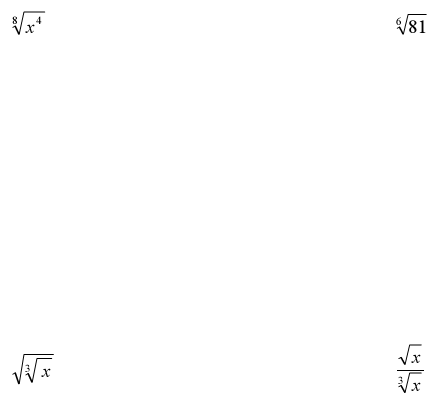
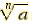 and
and
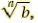
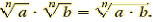





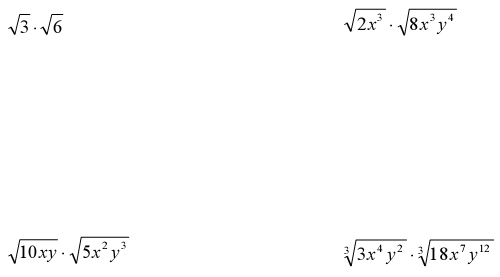
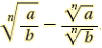
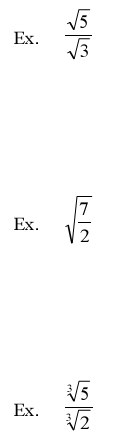

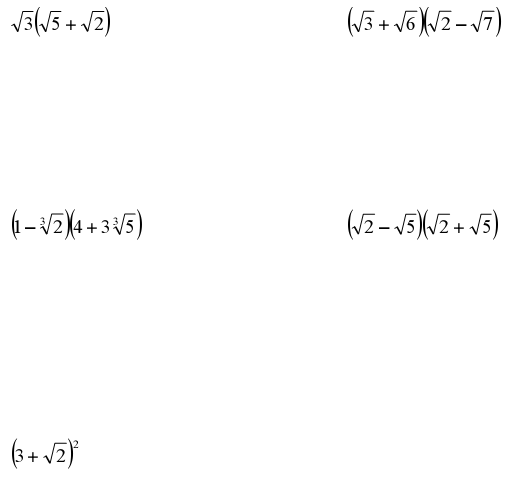
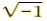 and
i2=-1
and
i2=-1
