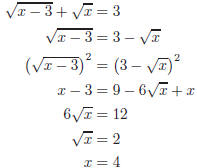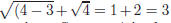|
Home |
Absolute Value and Radical Expressions, Equations and FunctionsBegin Exam. Directions: In each of the following exercises,
circle the “best” answer 1. Write interval notation for {x| − 7 ≤ x < 2}. (a) (−7, 2] (b) [−7, 2) (c) [−7, 2] 2. Find the solutions set for 3(6 − x) < 3x + 2. (a) (−∞, 10/3) (b) (2/3,+∞) (c) (−∞, 8/3) 3. Simplify (a) a (b) −a (c) |a| (d) 1/a (e) −1/a 4. Find the domain of the function
(a) {x|x ≥ 3} (b) {x|x ≤ 3} (c) {x|x < 3} 5. Simplify (a) x − 5 (b) |x| − 5 (c) |x − 5| 6. Approximate (a) 2469 (b) 111.108 (c) 7.536 (d) 5.927 (e) 6.581 7. Simplify:
8. Simplify:
9. Subtract and simplify:
Directions: Place the solution to each of the
following exercises on Exercise 1. Solve the inequality. Graph the
solution on a number Exercise 2. Solve the inequality with absolute
value. Graph the Exercise 3. Graph the system of linear inequalities
shading the appropriate Exercise 4. (a) Solve |2x + 5| = 3 (b) Rationalize the denominator and simplify:
Exercise 5. Solve:
Exercise 6. Solve:
Solutions to Quizzes Solution to Question 1: The graph of the inequality
−7 ≤ x < 2
Interval notation for the inequality {x| − 7 ≤ x < 2} is [−7, 2). Solution to Question 2:
The graph of the inequality x > 8/3 is given by
In interval notation the solution is (8/3,+∞). Solution to Question 3: Since the index is even
Solution to Question 4: Given
Solution to Question 5: Begin simplifying by
factoring under the Solution to Question 6: Use your calculator to find
The absolute value is not needed in the denominator since
y4 > 0 for Solution to Question 8: Use fractional exponents to simplify.
Solution to Question 9: Simplify the radicals
before combining like
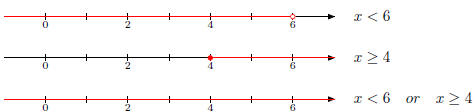
Solutions to Exercises Exercise 1. First solve each inequality separately. Graph each inequality and combine the inequalities for the “or” statement
The last number line shows the solution is all real
numbers. In set-builder Exercise 2. First rewrite the “less than”
inequality with absolute Now solving yields −2≤ −4x + 5 ≤ 2 The graph of the inequality 3/4 ≤ x ≤ 7/4 is given by
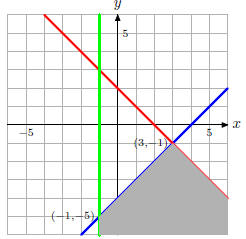
Exercise 3. Begin by finding the x−intercepts and
y−intercepts for
Plotting the intercepts and shading the appropriate
regions gives the
To solve the system Add E1 and E2 to eliminate y. This give Now substitute into E1 and solve for y to get The second vertex is a simple substitution of x = −1 into
the The other vertex is at (−1,−5). Exercise 3 Exercise 4(a) Rewrite the equation with absolute value as two equations. 2x + 5 =−3 or 2x + 5 = 3
Exercise 5. Remove the radical by squaring both sides.
Setting each factor equal to zero and solving gives Now must check each solution in the original equation. For x = −3 the left-hand side of the equation is
Exercise 6. Isolate one of the radicals and square
both sides to
Check the solution by substituting x = 4 into the original
equation. |
||||||||


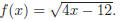
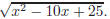
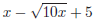
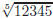 to
three decimal places.
to
three decimal places.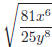
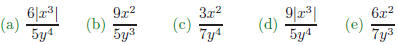
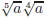
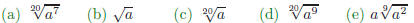
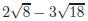
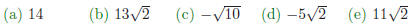
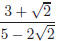
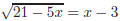
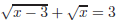

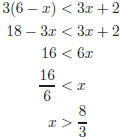
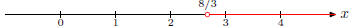
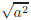 simplifies to
simplifies to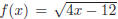 the function is
the function is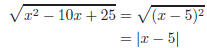
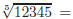
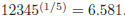
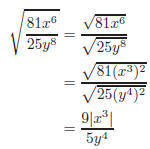
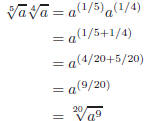
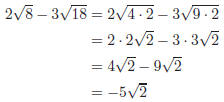

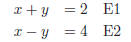
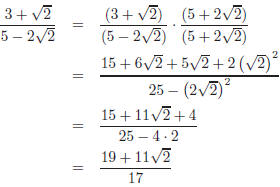
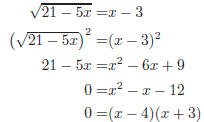
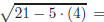
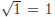 and the right-hand side of the equation is
(4) − 3 = 1. So
and the right-hand side of the equation is
(4) − 3 = 1. So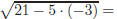
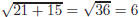 and the right-hand side of the
equation is (−3)−
and the right-hand side of the
equation is (−3)−