|
|
Rational Expressions
Simplifying Rational Expressions
To simplify a rational expression means to reduce it to lowest terms. From
working with fractions, you may
recall that simplifying is done by cancelling common factors. Therefore, the key
to simplifying rational
expressions (and to most problems involving rational expressions) is to factor
the polynomials whenever
possible.
Example 1: Write
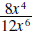 in reduced form.
in reduced form.
Solution: Factor the numbers and cancel common factors. Use properties of
exponents to help cancel
the x’s:
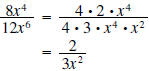
Example 2: Write
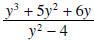 in reduced form. in reduced form.
Solution:
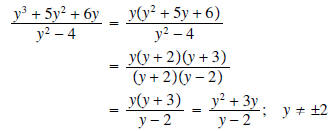
Question: Why is y ≠±2?
Answer: In order for our answer to be equivalent to the original fraction, the
variable must have the
same restrictions. Since y cannot equal ±2 in the original expression (the
denominator would then be zero), we
must restrict the domain of our answer in order for these fractions to be
equivalent.
Example 3: Write
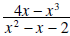 in reduced form.
in reduced form.
Solution:
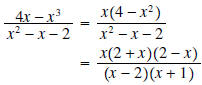
At this point, it doesn’t look like anything will cancel.
However, if we factor -1 from the last term in the
numerator, we obtain the following:
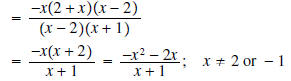
Question: What property of real numbers tells us
that
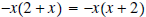 ?
?
Answer: The commutative property of addition.
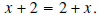
|