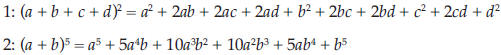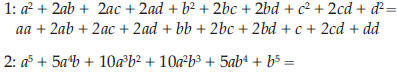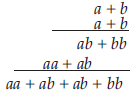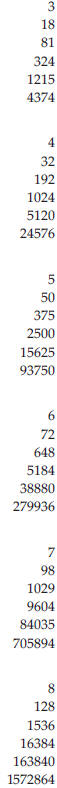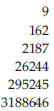|
|
Algebraic Expressions
Mathematics is often defined as the science of space and
number. …it was not until
the recent resonance of computers and mathematics that a more apt definition
became fully evident: mathematics is the science of patterns.
— Lynn Arthur Steen
Ada Dietz introduced a novel method of weave design in her seminal
monograph Algebraic Expressions in Handweaving [1]. Her idea was to use
multivariate polynomials (polynomials in several variables) raised to different
powers to produce sequences that could be used as the basis for design. Such
design sequences can be used as profile sequences, color sequences, and so on
[2-7].
Dietz Polynomials
The polynomials Ada Dietz used consist of the sum of variables with unit
coefficients raised to a power. An example is (a + b + c)3. Note: Standard
mathematical notation uses italic lowercase letters at the end of the alphabet,
such as x, y, and z, for variables, and roman lowercase letters at the beginning
of
the alphabet, such as a, b, and c for constants. The use of letters here is
deliberately different, since in many uses, variables correspond to blocks, for
which the first letters of the alphabet usually are used.
The number of variables used corresponds to the number of blocks desired,
while the power to which the polynomial is raised corresponds to the “degree
of interaction” among the blocks.
For example, in (a + b + c + d)2 there are four blocks, a, b, c, and d, with a
small
amount of interaction, while in (a + b)5 , there are two blocks, a and b, with a
large
amount of interaction.
Design sequences are constructed from such expressions in the following
way. First, the polynomial is multiplied out, combining like terms, to give the
individual terms:
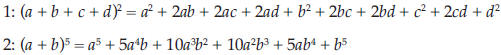
Next, powers are replaced by products of variables:
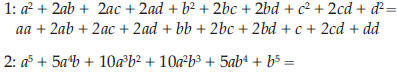
aaaaa + 5aaab + 10aaabb + 10aabbb + 5abbbb + bbbbb
Next, numerical coefficients are interpreted as repetitions of the variables
that follow them:
1: aa + 2ab + 2ac + 2ad + bb + 2bc + 2bd + cc +2cd + dd →
aa + abab + acac + adad + bb + bcbc + bdbd + cc + cdcd + dd
2: aaaaa + 5aaab + 10aaabb + 10aabbb + 5abbbb + bbbbb →
aaaaa + aaabaaabaaab + aaabbaaabbaaabbaaabbaaabbaaabbaaabbaaabbaaab_
baaabb + aabbbaabbbaabbbaabbbaabbbaabbbaabbbaabbbaabbbaabbb +
abbbbabbbbabbbbabbbbabbbb + bbbbb
An underscore indicates a term that is too long to fit on the current line and
is continued onto the next.
Note that this transformation produces a result that is not mathematically
equivalent to the previous expression, since, for example, abab = a2b2, not 2ab.
The
use of → above instead of = indicates the result is not mathematically
equivalent.
Finally, the terms are concatenated to produce a profile sequence:
1: aa + abab + acac + adad + bb + bcbc + bdbd + cc +cdcd + dd →
aaababacacadadbbbcbcbdbdcccdcddd
2: aaaaa + aaabaaabaaab + aaabbaaabbaaabbaaabbaaabbaaabbaaabbaaabbaaabbaaabb +
aabbbaabbbaabbbaabbbaabbbaabbbaabbbaabbbaabbbaabbb +
abbbbabbbbabbbbabbbbabbbb + bbbbb →
aaaaaaaaabaaaabaaaabaaaabaaaabaaabbaaabbaaabbaaabbaaabbaaabbaaabba_
aabbaaabbaaabbaabbbaabbbaabbbabbbaabbbaabbbaabbbaabbbaabbbaabbbabbbb_
abbbbabbbbabbbbabbbbbbbbb
Although the procedure described above is not mathematically sound, it is
unambiguous if somewhat arbitrary.
The actual variables used are just names and are used to stand for things like
blocks and colors.
The pattern of variables in the result depends on the ordering of the
variables and terms. Conventional mathematical practice is followed in the
development above. Variables in the polynomials are in alphabetical order from
left to right and products in terms are written in the order of the variables.
Furthermore, the variables in the terms are ordered lexically (in dictionary
order). For example, aa appears before aab, and aab appears before aabb. Other
orderings could be used, but for uniformity, strict lexical ordering is used in
the
examples here.
Computing Dietz Polynomials
What is going on in deriving design sequences from polynomials is easier
to see if the simplifications that usually are performed in multiplying out
products of polynomials are bypassed and do not use powers or combine like
terms.
A simple example is (a + b)2, which conventionally is multiplied out to give
a2 + 2ab + b2. Instead, the multiplication process, without the use of powers
and
combining like terms, looks like this
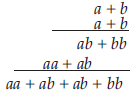
which directly yields aaababbb.
So the steps in the Dietz process amount to removing simplifications
usually made in polynomial arithmetic. When computing polynomial design
sequences by hand, the easiest method is to avoid the simplifications usually
made, going more directly to the end result (being careful to keep terms
separated and in the correct order).
Design Sequence Lengths
Dietz design sequences become quite long, especially when the power
(“degree of interaction”) is large. Here is a table showing lengths for various
numbers of variables and powers:
Sequences whose lengths are greater than several hundred
are not good
candidates for weave design, although parts of them may be.
Interlacement Patterns
There are many ways these sequences can be used in design, a subject we’ll
take up in a subsequent article.
An understanding of the nature of these sequences can be obtained by
using them as threading and treadling sequences.
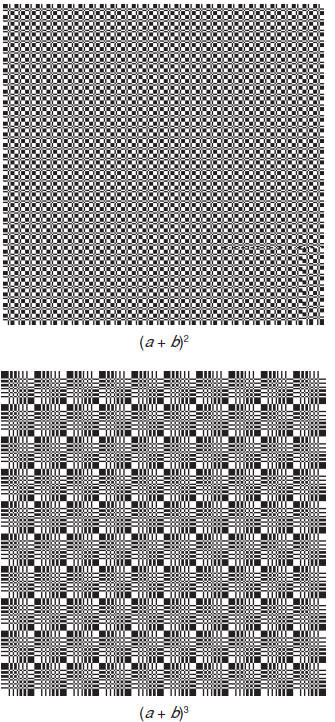
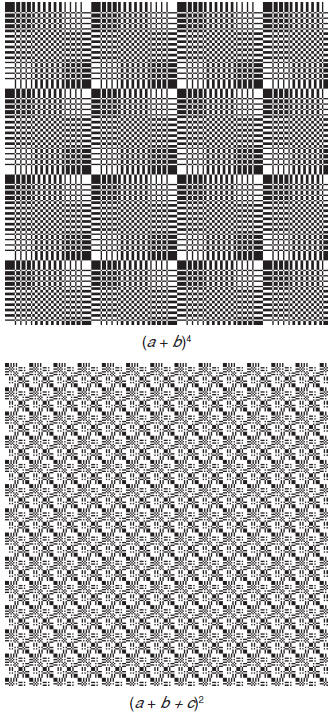
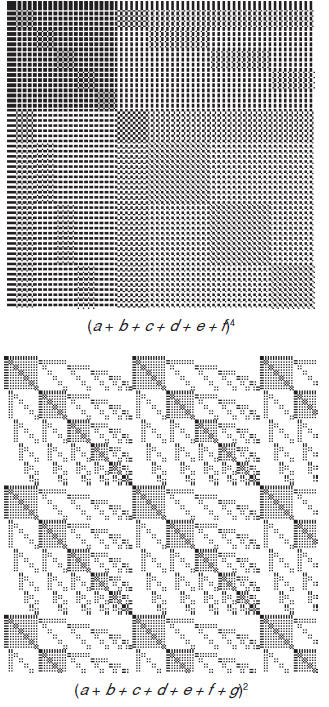
Interlacement patterns for patterns (drawdown images) for various Dietz
polynomials are shown on the following pages. In these patterns, the variables
a, b, c, … are assigned the shafts 1, 2, 3, … . Direct tie-ups are used and the
treadling is as drawn in.
Note how the patterns change down the columns as the powers increase
and across the rows of successive pages as the number of variables (and hence
shafts and treadles) increases.
The patterns show 240 ends and picks. As the power and number of
variables increase, some patterns do not show a full repeat. See the table of
sequence lengths given on the previous page. [More to come.]
Examples









|