Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Rational Expressions and Functions: Multiplying and Dividing

Rational Expressions

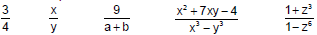
Rational Functions

Simplifying Rational Expressions

1.Write the numerator and denominator in factored form.
2.Divide out all common factors in the numerator and denominator.
3.Multiply the remaining factors in the numerator and the
remaining factors in the denominator.

FYI

The binomial a –b is the opposite of the binomial b –a.
Algebraically, write a –b as–(b –a) or –1(b –a).

Example 1

Find the function values indicated, provided the value exists.
State the domain of the function.


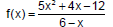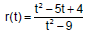f(0)	r(2)
f(-1)	r(-3)
Domain:	Domain:

Rule for Multiplying Rational Expressions

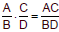, where A, B, C, and D are polynomials where B, D ≠ 0.

Example 2
Multiply. Do not simplify. Assume that all denominators are nonzero.

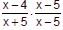
Example 3
Simplify by removing a factor equal to 1.

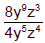
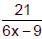Example 4
Write in simplified form. List all restrictions on the domain.


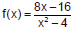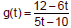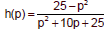Restrictions:	Restrictions:	Restrictions:

Example 5
Multiply and, if possible, simplify.

Rule for Dividing Rational Expressions

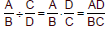where A, B, C, and D are polynomials where B, C, D ≠0.

Example 6
Divide and, if possible, simplify.

Example 7
Divide and, if possible, simplify.

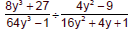Example 8
Write in simplified form. List all restrictions on the domain.


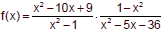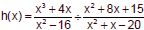Restrictions:	Restrictions:

Example 9
Perform the indicated operations and, if possible, simplify.

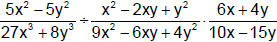Example 10
Find and explain the mistake.
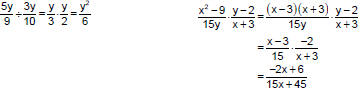