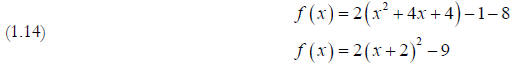Quadratic Expressions ,Equations and
Functions
Topics
This document gives a brief introduction to quadratics. Your text has more
details, but this should
give you the basics. We’ll cover
o Quadratic Expressions and working with them
o Quadratics Equations, and how to solve by
o Factoring
o Completing the square
o Quadratic Formula
o Solving graphically.
o Quadratic Functions
o Important features.
o How to find them by rearranging in standard form.
Quadratic Expressions
A quadratic expression is the building block for quadratic equations and
functions. You need to be
able to recognize them and work with them in order so solve equations and graph
functions.
A general quadratic expression is of the form
(1.1) ax2 + bx + c
Where a,b, and c are constants. The only restriction is
that a is not zero (otherwise, you have no x2
term).
You already met these in chapter 5. for example.

Some of them can be factored, for example:

But sadly, most of them can’t be factored. When factoring
is not possible, we need to use more
advanced methods.
A fundamental skill in this regard is completing the square. This will be used
in solving quadratic
equations and graphing quadratic functions.
Completing the square:
The basic idea is to take the part of the quadratic with the x2 and x terms
and, by adding an
appropriate constant, to turn it into a perfect square. When the coefficient of
x2 is 1, we find the
right constant by halving the coefficient of x and then squaring it.
Example: Complete the square for x2 + 6x
Solution: The coefficient of x is 6. Half of that is 3, and squaring you get 9.
The constant to add is
9, so we complete the square like this:
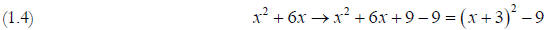
Notice that I “borrow” a 9 to complete the square, so I
must subtract it off at the end of the
expression. If we were solving an equation, we could instead add the same amount
to both sides so
that we don’t mess it up.
the coefficient of the squared term isn’t 1, you need to
be careful:
Example: Complete the square for 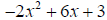
Solution: First factor the coefficient of x2 out of both the x2 and x2 terms.
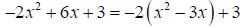
Now complete the square, but don’t forget to do the
opposite of whatever extra bit you put in at the
end of the expression.
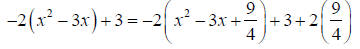
Finally tidy it up:
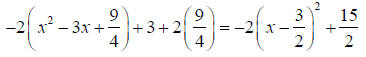
Quadratic Equations
Completing the square gives us a new technique for solving quadratic equations.
In fact, we have a
range of methods we can use:
o In simple cases we can solve by Factoring
o We now have Completing the square- see below.
o The Quadratic Formula is a formula that can be proved from completing the
square. It
gives us one messy formula for the answer. See below.
o Finally, as in previous topics we can solve the equation graphically. For
example, to
solve 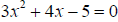 , we can graph , we can graph
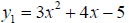 and find the x intercept, and find the x intercept,
Solving Quadratic Equations by Completing the Square
Example: Solve the equation x2 +10x − 3 = 0 by completing the square.
Solution: I’ll move the constant to the other side. This is optional, but it’s
less cluttered for when I
complete the square.

Now, complete the square, but don’t forget to add the same
thing to both sides.

Take the square root of both sides.

This is the answer in exact form. You can get 2 decimal
answers (in this case) by typing them in to
your calculator.
Quadratic equations don’t always have two real solutions.
In fact, they can have either:
o Two real solutions
o One real solutions
o No real solutions, but two complex solutions.
This is made clearer by the quadratic formula which we do
next.
Solving Quadratic Equations by The Quadratic Formula
It’s possible, if a bit tedious, to work out the general case of completing the
square for any quadratic
equation of the form

The formula we get is a bit messy, so when you’re working
with it be patient. The solution is

So to get the solutions you just plug a, b and c into the
formula and work out the two answers. This
sounds simple, but there are two frequent errors.
o You must have everything on one side before you start.
If you have e.g. x2 +10x = 6 , move
everything to one side first, so you have x2 +10x − 6 = 0. Otherwise your
values for a,b, and
c will be wrong.
o Be patient when working out the final answer. It’s best
to do it in stages rather than typing it
into your calculator as once. Start with the radicand first, and store it (or
write it down).
Different Types of Solutions and the “Discriminant”
The bit under the square root in the formula: b2 − 4ac , is called the “Discriminant”,
because it
“discriminates” or sorts out the different types of solution you can get.
o If b2 − 4ac is positive, the equation has two real solutions (they may be
messy decimals, but at
least you can find them)
o If b2 − 4ac is zero, the equation has one real solution.
o If b2 − 4ac is negative, the equation has two complex solutions.
Example: For the quadratic equation x2 + 3x + 6 =
0
1. Use the discriminant to decide what types of solution the equation has
2. Find the solution or solutions, and write them in simplest form.
Solution:
1. The discriminant is 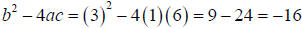 which is negative. So which is negative. So
there’s two complex solutions.
2. The solutions are:
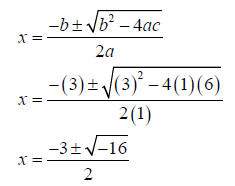
Now we should simplify this. Since
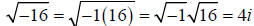 , we have , we have
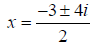
So the final answers are
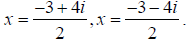
Graphing Quadratic Functions.
A quadratic function is the graph of a quadratic expression. For example:

You know from before the shape of a quadratic function is
either a “hill” or a “valley”, with which
one being determined by the coefficient of x2 . If the coefficient is positive,
it’s a valley. For
example, 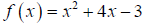 looks like this: looks like this:
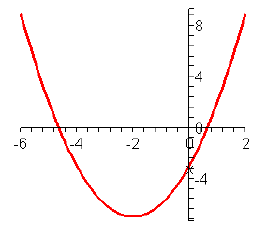
You can see the above graph reach it’s lowest point at
x=-2. By plugging in x=-2 into the function,
you also find the y co-ordinate is -7. So the lowest point of the graph is
(-2,7).
This point is called the vertex of the quadratic function.
Also, You can see the two halves of the
graph on either side of the vertex are mirror images of each other. The vertical
line through the
vertex is called the axis of symmetry of the graph. Here it’s the vertical line
x=-2. So the equation of
the axis of symmetry is easy to get once you have the vertex – you just use the
x co-ordinate.
In the example above we found the vertex by graphing and
having a look at the graph. However
there’s a more systematic way of finding these features from the function. To do
this, you must use
completing the square to rearrange the function in standard form. The standard
form of a quadratic is:

where a,h and k are constants. This might look like at odd
way to arrange your graph. But the vertex
is just (h,k) so you can immediately tell where the vertex is. Also, a tells you
the shape. If it’s positive
the graph is a valley, negative it’s a hill. For example, for the function

Since h=2 and k=4, the vertex is at (2,4). Also since a is
-3 which is negative, it’s a hill.
Here’s an example where we’ll rearrange the function.
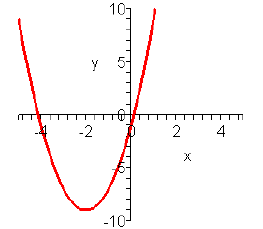
Example: Rearrange the function f ( x) = 2x2 + 6x
−1 in standard form. Use this form to
determine the vertex, axis of symmetry, and the overall shape.
Solution: We rearrange by completing the square.
First factor the 2 out of just the x2 and x terms.

Now to complete the square we must halve 2 and square it,
giving 4. But since the 4 is being multiplied
by 2, we must subtract 8, not 4, so as not to change the function. So:
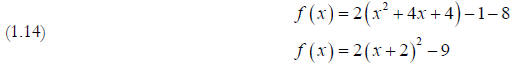
This quadratic has it’s vertex at (h,k) = (-2,-9), it’s
axis of symmetry is x=-2, and it’s a valley since
a=2 is positive.
Let’s confirm all this by graphing it: You can see the vertex is where we
predicted:
That’s it from me! Hope this helps.
|




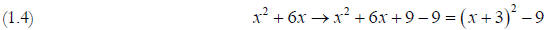
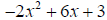
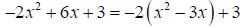
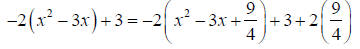
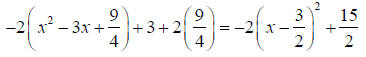
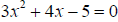 , we can graph
, we can graph
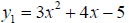 and find the x intercept,
and find the x intercept,




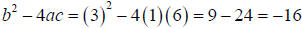 which is negative. So
which is negative. So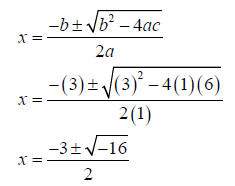
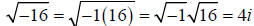 , we have
, we have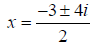
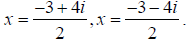

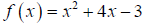 looks like this:
looks like this: