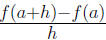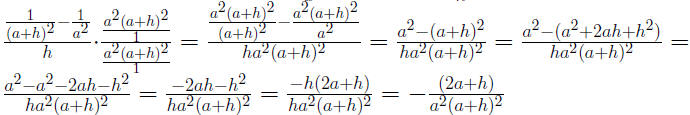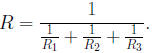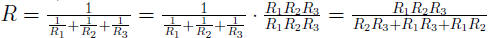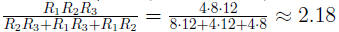|
|
rational expressions
Complex rational expressions contain fractions within
fractions. This is un-
desirable. We now learn how to turn complex rational expressions into the
preferable rational expression.
When would we encounter such a situation?
If 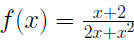 and consider and consider
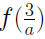 , Then , Then 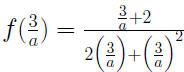
We will learn two ways of accomplishing our goal. You may choose the one
you prefer.
Property 0.1 Simplify a Complex Rational Expresion by Multiplying by
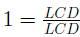
1. Find the LCD of all rational expressions within the complex rational
expression.
2. Multiply both the numerator and denominator of the complex rational
expression by this LCD.
3. Use the distributive property and multiply each term in the numera-
tor and denominator by the LCD. Simplify each term. No fractional
expressions should remain within the main fraction.
4. Factor and simplify.
Example 0.1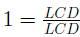
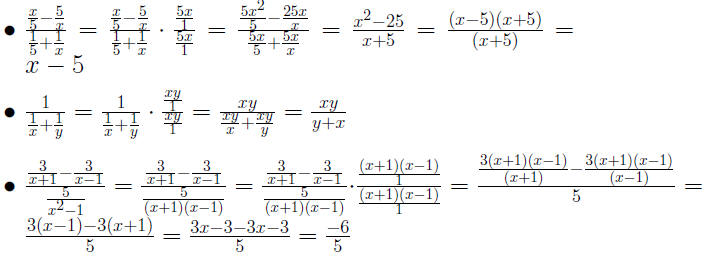
Property 0.2 Simplify a Complex Rational Expresion
by Dividing
1. Add or subtract to get a single expression in the numerator.
2. Add or subtract to get a single expression in the denominator.
3. Perform the division indicated by the main fraction bar. That is, invert
the denominator of the complex rational expression and multiply.
4. Simplify.
Example 0.2 Simplify a Complex Rational Expresion by Dividing
Example 0.3 Suppose
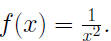 Find Find 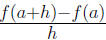
Example 0.4 If three resistors with resistances R1,
R2, and R1 are con-
nected in parrallel, their combined resistance, R, is given by the formula
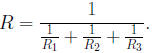
Simplify the complex rational expression on the right side
of the formula.
Then find R, to the nearest hundredth of an ohm, when R1 is 4
ohms, R2 is
8 ohms, and R3 is 12 ohms.
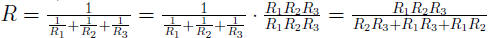
when R1 is 4 ohms, R2 is 8 ohms, and
R3 is 12 ohms
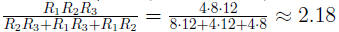
|


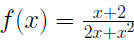 and consider
and consider
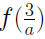 , Then
, Then 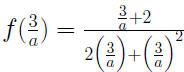
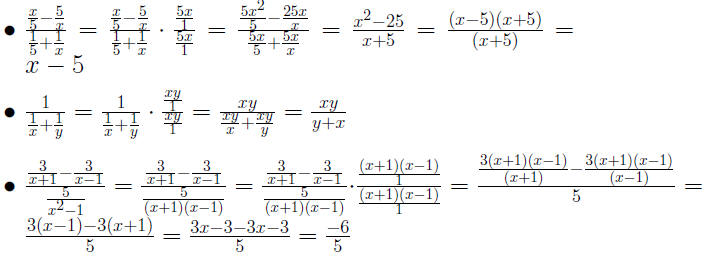
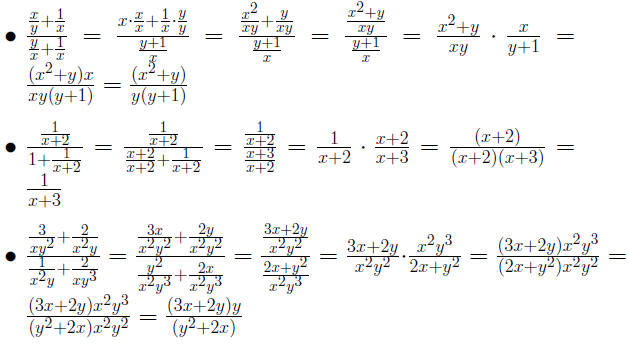
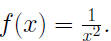 Find
Find