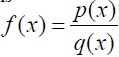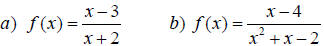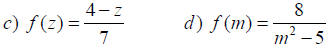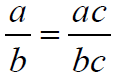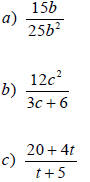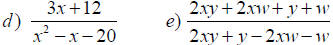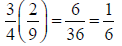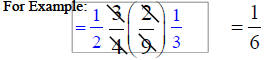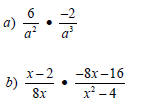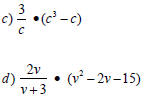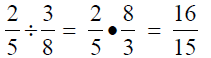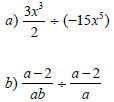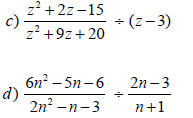Rational Expressions & Functions
Objective: To define and simplify rational
expressions, describe their domains, and
multiply and divide rational expressions.
Definition 1
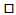 Rational expression – an algebraic Rational expression – an algebraic
__________ with a variable
Examples
Remember: Denominator cannot equal zero!
Definition 2
 rational function – a __________ of two rational function – a __________ of two
polynomials
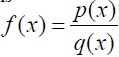
where p(x) and q(x) are polynomials and
where q(x) is not zero.
Find all numbers in the domain of each
rational function. Write using interval
notation.
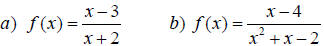
Find all numbers in the domain of each
rational function. Write using interval
notation.
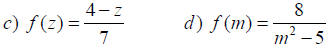
Fundamental Property
of Rational Numbers
 See bottom of page 415. See bottom of page 415.
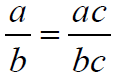
Simplifying a Rational Expression
1. ______ numerator and denominator.
2. Apply the fundamental property.
(__________ common factors.)
3. __________.
4. Note exclusions. (values that make
denominator equal zero)
Watch & think.
Simplify. Note exclusions.

EXAMPLES – Simplify.
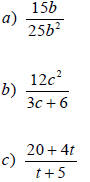
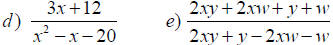
Opposite Factors
 After factoring, if you have “__________ After factoring, if you have “__________
factors”, you can factor out –1 and then
cancel.
 For example: (x - 3) & (3 - x) are For example: (x - 3) & (3 - x) are
opposites.
 - (3 - x) =(-3 + x)= (x – 3) - (3 - x) =(-3 + x)= (x – 3)
Simplify.
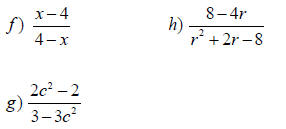
Multiplying and Dividing
Rational Expressions
Page 418
Review of Multiplying Fractions
 Rule: top x top Rule: top x top
bottom x bottom
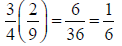
Want to Cancel before Multiplying? Fine!
(It’s like reducing first!) But…
Cancel only top to bottom!
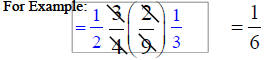
Multiplying Rational Expressions
1. __________, if possible.
2. Cancel out common __________ on top &
bottom.
3. Multiply remaining factors.
4. Simplify, if needed.
Multiplication Examples
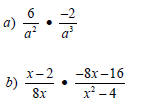
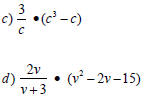
Dividing Algebraic Fractions
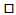 Reminder: When dividing fractions, Reminder: When dividing fractions,
multiply by the __________. (Flip the
second fraction and multiply.)
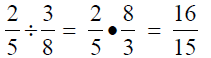
Steps for Dividing
Rational Expressions
1. Flip second fraction and change division sign
to multiplication sign.
2. Follow same steps as with multiplication.
Division Examples
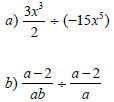
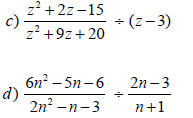
IMPORTANT REMINDER!!!!
 You can only cancel a monomial with a You can only cancel a monomial with a
monomial, or a binomial with a binomial, etc.
 You CANNOT cancel part of a polynomial You CANNOT cancel part of a polynomial
with a monomial!!!
 You MUST __________ before canceling!! You MUST __________ before canceling!!
SUMMARY
 Factor, cancel, multiply. Factor, cancel, multiply.
 If dividing, multiply by reciprocal of 2nd If dividing, multiply by reciprocal of 2nd
fraction.
|


 Rational expression – an algebraic
Rational expression – an algebraic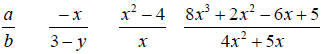
 rational function – a __________ of two
rational function – a __________ of two