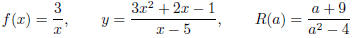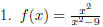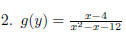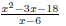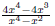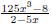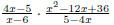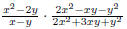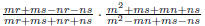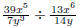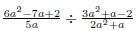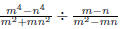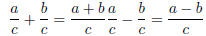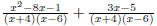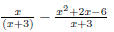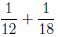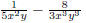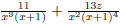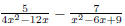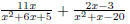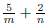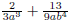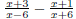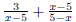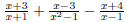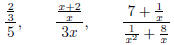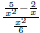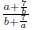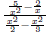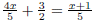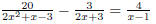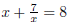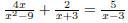|
Home |
Rational Expressions and Equations6.1 Introduction to Rational Functions and Expressions REMARK 1. We will be making extensive use of the
polynomial factoring that we learned in the Definition 1. A rational expression is an
expression of the form p/q , where p and q are polynomials EX 1. The following are examples of rational expressions:
6.1.1 Domains of Rational Functions Functions involving rational expressions are called rational functions. More specifically: Definition 2. A rational function is a function of
the form EX 2.
With rational functions we need to be careful about the
domain. Remember, the domain is the Consider the rst example from above f(x) = 3/x can we let x = 0? If not, why not? In general, when dealing with a rational function, the
domain is all the numbers except those REMARK 2. To nd the domain of a rational function,
nd all values which make the denominator EX 3. Find the domain of the following rational functions.
REMARK 3. Note that we didn't use the numerator at all when nding the domain. 6.1.2 Simplifying Rational Expressions De nition 3. A rational expression is simpli ed
when the numerator and denominator have no REMARK 4. This concept and process is identical to
the concept of simplifying a fraction. EX 4. - 2. Simplify 3. Simplify Common Errors Watch out for the following common errors: 6.1.3 Multiplying and Dividing Rational Expressions 1. Factor al the numerators and denominators completely. 2. Divide out the common factors. We then multiply the numerators and denominators. EX 5. - 2. Multiply: 3. Multiply: To divide rational expressions it is just like dividing fractions. We just multiply by the reciprocal. EX 6. - 2. Divide: 3. Divide: 6.2 Addition and Subtraction of Rational Expressions In the last section we learned how to multiply and divide
rational expressions. We now shift to 6.2.1 With Common Denominators
Remember to simplify after adding or subtracting. EX 7. - 1. Add: 2. Subtract: Caution: When subtracting be sure to subtract the entire numerator. 6.2.2 Finding the Least Common Denominator (LCD) In order to add and subtract rational expressions with
unlike denominators, it will be necessary EX 8. -
2. Find the LCD of 1 3. Find the LCD of 4. Find the LCD of 5. Find the LCD of 6.2.3 Add and Subtract Expressions with Unlike
Denominators 1. Find the LCD 2. Rewrite each fraction as an equivalent fraction with the LCD 3. Leave denominator factored, multiply out the numerator. 4. Add or subtract 5. If possible, simplify the results. EX 9. - 2. Add: 3. Subtract: 4. Add: 5. Subtract: 6. Simplify: 6.3 Complex Fractions A complex fraction is one that has a rational expression
in its numerator or denominator or both.
Our goal will be to simplify complex fractions, which means to rewrite it so it is not complex. 6.3.1 Simplify Complex Fractions by Multiplying by a the LCD One way to simplify these messes is to multiply the
numerator and denominator by the LCD. 1. Find the LCD of all the fractions appearing within the complex fraction. 2. Multiply the numerator and denominator of the complex fraction by the LCD found in step 1. 3. Simplify. EX 11. - 2. Simplify 6.3.2 Simplify by Simplifying the Numerator and
Denominator 6.4 Solving Rational Equations 1. Determine the LCD of all rational expressions. 2. Multiply both sides of the equation by the LCD. 3. Combine like terms on either side. 4. Solve using methods discussed before. (Note: if the
previous steps were done properly, there 5. Check the solutions found in the original equations. EX 13. Solve: REMARK 5. If a variable appears in the denominator
of the original expression, it is important EX 14. - 2. Solve: 3. Solve: |


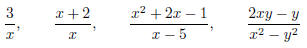
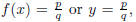 where p and q
where p and q