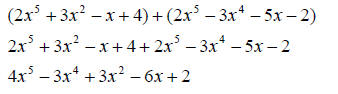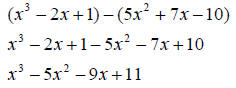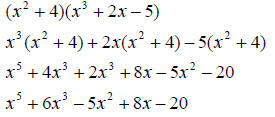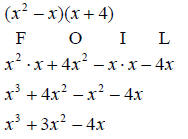|
Home |
Polynomial ExpressionsA polynomial is an expression which involves various
powers of a variable. Some examples are:
Here the coefficients (a's) can be any real number. The number n, which is an integer, is known as the degree of the polynomial. EX. Classifying PolynomialsPolynomials can be classified based on the degree (largest power), or based on the number of terms. 1 term = monomial EX. _____________________________________________________________ Basic Operations on PolynomialsJust like with numbers, we often want to add, subtract, multiply and divide polynomials. Addition Adding polynomials is simply collecting like terms EX.
Subtraction: To subtract two polynomials, you simply use the distributive law, then collect like terms. EX.
Notice you distribute the minus sign. Multiplication: While adding and subtracting were fairly easy, multiply two polynomials can quickly become a headache. To multiply you must repeatedly apply the distributive law, then collect like terms. EX.
Notice that the distributive law was applied four times to complete that single multiplication Division: FOILThere is a special case for multiplying polynomials, which occurs when you multiply a binomial times a binomial. In this case it is easier to use FOIL. EX.
|


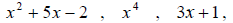 and 5. The general form for a polynomial is:
and 5. The general form for a polynomial is: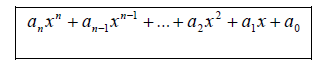
 is a polynomial of
degree 3, with leading coefficient 5, and constant term -2.
is a polynomial of
degree 3, with leading coefficient 5, and constant term -2.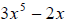 is a binomial of
degree 5.
is a binomial of
degree 5.